тивление Zg группы параллельно включенных идеализированных

пассивных двухполюсников:

N . М

+1 + 1-7-- (2-130)

Выражения, подобные (2.129) и (2.130), можно получить для комплексной проводимости и комплексного сопротивления любого участка цепи, являющегося параллельным соединением произвольного количества идеализированных пассивных двухполюсников с заданным комплексным входным сопротивлением Zj или комплексной входной проводимостью Vf.

t=l ЭК 11

где N - число параллельно включенных двухполюсников.

Используя (2.131), найдем выражение для комплексного входного сопротивления участка цепи, представляющего собой параллельное соединение двух элементов с комплексными сопротивлениями Zi и Z:

Z,„ = ZjZj{Zj + Zj). (2.132)

Участки цепей со смешанным соединением элементов

Правила преобразования участков цепей с параллельным или последовательным соединением элементов могут быть применены и для преобразования пассивных участков цепей со смешанным соединением элементов. Преобразование таких участков, представляющих собой сочетание групп параллельно или последовательно включенных элементов, обычно производят в несколько этапов, на каждом из которых группу параллельно включенных элементов заменяют одним двухполюсником, комплексная проводимость которого равна сумме комплексных проводимостей параллельно включенных элементов, а группу последовательно включенных элементов - одним двухполюсником, комплексное сопротивление которого равно сумме комплексных сопротив-лен1)й всех последовательно включенных элементов.

Пример 2.8. Рассмотрим преобразование участка идеализированной цепи со смешанным соединением элементов (рис. 2.31, а), содержащего группу параллельно включенных элементов (Zg, Z) и группу последовательно включенных элементов (Z], Zj). Заменяя параллельно включенные элементы Zj и z4 одним элементом с комплексным сопротивлением

эк1 =3 4/(3+4).

получим преобразованную схему цепи (рис. 2.31, б) с тремя последовательно включенными элементами: Zy Zj и Zoki- Заменяя эти элементы одним с комплексным сопротивлением ~

2э„2 = Zj + Z + ZaKi = Zi + Zj -I z3 ZJ(Z, + Z,),

i z,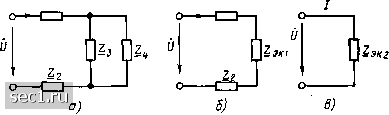

Рис. 2.31. К примеру 2.8

приходим к простейшей преобразованной схеме рассматриваемого участка цепи с одним элементом 2э„2 (рис. 2.31, в).

Пример 2.9. Определим эквивалентную индуктивность цепи с параметрами элементов Lj =- Lj = l3 - 300 мкГн, схема которой приведена на рис. 2.32.

Участок цепи с тремя параллельно включенными одинаковыми индуктивно-стями = L3 = Li обладает эквивалентной индуктивностью, в три раза меньшей, чем каолдая из параллельно включенных индуктивностей, 1э„1 = = 100 мкГн. Этот участок включен последовательно с индуктивностью L, поэтому искомая эквивалентная индуктивность

-эк2-=Н-эк1 = 400 мкГн.

Пример 2.10. Определим комплексное входное сопротивление участка цепи с параметрами элементов R -- 1,5 кОм, Q = 40 пФ, = 10 пФ, с3 = 50 пФ частотой внешнего воздействия f = 1,2 МГц (рис. 2.33).

Параллельно включенные емкости и с3 могут быть заменены одной эквивалентной емкостью

Сэк1 СИ-Сз = 60 пФ.

Емкости Ci и Сдк1, включенные последовательно, заменим одной емкостью

Сэк2=-С1Сэ„1/(С1 + Сэ„1)-=24 пФ.

Получаем преобразованную цепь (рис. 2.33, б). В результате комплексное входное сопротивление цепи на частоте f = 1,2 МГц

/?- (2п/Сэ„2)= 1,5-/5,53, кОм.

Из рассмотренных примеров следует, что в результате объединения групп последовательно и параллельно включенных элементов происходит постепенное «сворачивание» цепи, причем участок со смеишн-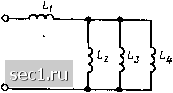

ЭК г

Рис. 2.32. К примеру 2.9

а) 5)

Рис. 2.33. К примеру 2.10

ным соединением пассивных элежнтов, имеющий два внешних вывода (пассивный двухполюсник), в конечном счете, может быть заменен одним элементом, комплексное сопротивление которого равно входному сопротивлению исходного участка цепи.

К цепям со смешанным соединением элементов относятся цепные или лестничные цепи, входное сопротивление или входная проводимость которых могут быть представлены в виде цепной

(непрерывной) дроби, т. е. с помощью выражения типа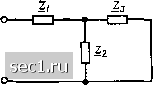

Рис. 2.34. Схема простейшей лестничной цепи

Коэффициенты ai, а, аы называются элементами цепной дроби. Число элементов дроби N может быть конечным (конечная цепная дробь) или бесконечным (бесконечная цепная дробь). Рассмотрим простейшую лестничную цепь (рис. 2.34). Нетрудно установить, что входное сопротивление этой цепи

- Z2 + z3 l/z,+ l/23 •

Заменяя в этом выражении сопротивление элемента Zj его проводимостью f2 == I/Z2, получаем окончательно

Z = Zi

n-bl/Z3

Таким образом, входное сопротивление рассматриваемой цепи может быть представлено в виде конечной цепной дроби, элементы которой fli, аа, из равны соответственно Zj, Yj, Z.,. Используя аналогичные преобразования, можно представить в виде цепной дроби и входное сопротивление лестничной цепи более общего вида (рис. 2.35, а):

Z = Zi-f

(2.133)

Yn-x +1/2,

Таким образом, число элементов цепной дроби равно числу идеализированных двухполюсных элементов, образующих лестничную цепь, причем элементами цепной дроби являкггся комплексные сопротивления двухполюсников, образующих продольные ветви лестничной цепи (Zj, z3,..., Zn), и комплексные проводимости двухполюсников, входящих в поперечные ветви (К,, К4,..., Yn-ij-