Первое слагаемое в каждом из выражений (2.153) представляет собой э.д.с. самоиндукции, второе - э. д. с. взаимоиндукции. Преобразуем выражения (2.153), формально умножив и разделив каждое из слагаемых на di- или di:

\ d(i dt di dt j

(Ibl. Jb- Ли Ail.] (2 154)

V di dt dii dt I У >

В индуктивных катушках без ферромагнитных сердечников магнитные потоки самоиндукции и взаимоиндукции пропорциональны вызывающим их токам, поэтому производные потокосцеплений потокам могут быть заменены отношением соответствующих величин. Индуктивность каждой катушки Li или La есть отношение потокосцепления самоиндукции к вызвавшему его току:

J=J=J!?i Iu-; L, = i = i=-M. (2155)

Взаимная индуктивность между катушками М- и TWai - это отношение потокосцепления взаимоиндукции к вызвавшему его току:

•12 ----:---:-> --Т----:- "--:-•

(2.156)

Связанные индуктивные катушки, у которых потоки самоиндукции и взаимоиндукции пропорциональны вызвавшим их токам и, следовательно, величины Lj, L, М и М не зависят от ii и ta. называются катушками с линейной индуктивностью. Для них всегда выполняется условие Jii = iJix, поэтому

Mi = Mi = M. (2.157)

Взаимную индуктивность выражают в генри (Гн). С учетом введенных обозначений (2.155), (2.156), (2.157) э.д.с, наводимые в каждой из катушек:

Переходя от э.д. с. к напряжениям на зажимах связанных индуктивных катушек, получаем окончательно

/ (2.158)

dt dt

В теории электрических цепей рассмотрение реальных элементов - связанных индуктивных катушек - заменяют рассмотрением их упрощенных моделей - связанных индуктивностей. Связанные

5 131

индуктивности представляют собой идеализированные элементы, отражающие основные явления, которые присущи связанным индуктивным катушкам: самоиндукцию и взаимоиндукцию, или, в конечном счете, явления запасания энергии в магнитном поле. В связанных индуктивностях не происходит запасания энергии в электрическом поле или преобразования ее в другие виды энергии, что всегда в той или иной мере имеет место в реальных элементах.

Ток и напряжение на зажимах связанных индуктивностей задаются выражениями (2.158). Если рассматриваемая цепь содержит п связанных индуктивностей, то зависимость между токами и напряжениями на их зажимах определяется системой уравнений:

"2 = ±M2i- + L2 -±...±Л12„ -; (2.159)

at dt dt

где Mij = Mji - взаимная индуктивность между t-й и / -й связанными индуктивностями.

Уравнения (2.158), (2.159) следует рассматривать как компонентные уравнения ветвей, содержащих связанные индуктивности.

Понятие об одноименных зажимах

При анализе цепей с взаимной индуктивностью возникает задача определить, каким образом (согласно или встречно) по отношению к выбранным условным положительным направлениям токов включены рассматриваемые индуктивные катушки и в соответствие с этим какой знак (плюс или минус) необходимо использовать в выражениях (2.158), (2.159). Если конструкции индуктивных катушек, в частности направления их намотки, известны, а направления токов заданы, то для выбора знака в выражениях (2.158), (2.159) или (2.150) - (2.154) достаточно, воспользовавшись правилом буравчика (правохо-дового винта), определить направления магнитных потоков самоиндукции каждой из катушек. Например, применяя правило буравчика, устанавливаем, что у катушек, изображенных на рис. 2.43, а, направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы, а у катушек, изображенных на рис. 2.43, б, - противоположны.

При вычерчивании принципиальных электрических схем цепей с взаимной индуктивностью индуктивные катушки изображают с помощью условных графических обозначений, которые не отражают особенностей их конструкции. Для выяснения, является ли данное включение катушек согласным или встречным, вводят понятие одноименных зажимов связанных индуктивных катушек.

Одноименными зажимами двух связанных индуктивных катушек называется пара зажимов, выбранных таким образом, что при одинаковых относительнр этих зажимов направлениях токов катушек магнитные потоки самоиндукции и взаимоиндукции в каждой из них суммируются. Одноименные зажимы индуктивных катушек помечают одинаковыми значками (буквами ник, точками, звездочками, треугольниками и т. п.), проставляемыми в непосредственной близости к соответствующим зажимам. Так, на рис. 2.43, а звездочками отмечены одноименные зажимы 1 к 2. Вторую пару одноименных зажимов этих катушек образуют зажимы Г и 2, специально не обозначенные, так как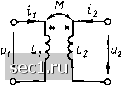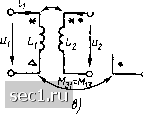

Рис. 2.44. Условные графические обозначения связанных индуктивностей на эквивалентных схемах

ДЛЯ решения вопроса о том, является ли заданное включение согласным или встречным, достаточно обозначить одну пару одноцменных зажимов. На рис. 2.43, б точками обозначены одноименные зажимы 1 и 2.

Аналогично поступают и при построении эквивалентных схем электрических пеней с взаимными индуктивностями. Условное графическое изображение связанных индуктивностей, используемое при построении таких схем, показано на рис. 2.44, а. Когда общим магнитным потоком связано не две, а большее количество индуктивностей, одноименные зажимы каждой из пар обозначают с помощью различных значков (рис. 2.44, в).

Итак, если токи связанных индуктивностей одинаково ориентированы относительно одноименных зажимов, то такое включение является согласным и в выражениях (2.158) следует использовать знак плюс; в противном случае, включение является встречным и необходимо использовать знак минус (величина М при этом считается положительной). Например, индуктивности Li и на рис. 2.44, а и Li и на рис. 2.44, б включены согласно, а индуктивности и L,Li и (рис. 2.44, в) включены встречно.

До сих пор рассматривались только соосно расположенные индуктивные катушки. В общем случае, когда направления осей связанных индуктивных катушек не совпадают, при выборе способа их включения используют несколько иной подход. При этом в выражениях (2.158) берут знак плюс, а взаимную индуктивность рассчитавают по формуле

М =- Мщах cos а,

где а - угол между направлением магнитных потоков самоиндукции и взаимоиндукции в центре катушек.