Коэффициент связи между индуктивными катушками

Из качественного рассмотрения процессов в связанных индуктивных катушках следует, что чем сильнее связаны катушки, т. е. чем большая часть магнитного потока, создаваемого током каждой из них, пронизывает другую катушку, тем выше взаимная индуктивность. Однако при этом не ясно, как связана взаимная индуктивность с индуктивностями катушек, и чем определяется максимальное значение М. Введем новую величину, количественно характеризуюш,ую степень связи между катушками -- коэффициент связи. Коэффициент связи км представляет собой среднее геометрическое из отношений потока взаимоиндукции к потоку самоиндукции каждой из катушек:

км = У Ф21/(Ф11 Ф22). (2.160)

Представляя магнитный поток самоиндукции каждой из катушек в виде суммы потока рассеяния этой катушки и потока взаимоиндук-дии другой катушки (2.149), получаем

км = УФхг Ф21/(Ф21 + Фя.) (Ф12 + Ф52). (2161)

Из выражения (2.161) видно, что значения коэффициента связи лежат в пределах

0<йм<1, (2.162)

причем км так = 1 только тогда, когда потоки рассеяния обеих катушек равны нулю, или, другими словами, когда магнитный поток, создаваемый током одной катушки, полностью пронизывает другую катушку. Коэффициент связи определяется конструкцией катушки и практически всегда меньше единицы.

Коэффициент связи км можно выразить через индуктивности связанных катушек и их взаимную индуктивность. Подставляя в (2.160) выражения для потоков самоиндукции Фц, Ф22 и взаимоиндукции i2> Фаъ полученные из (2.155), (2.156), находим

откуда

М=кмУ!. (2.163)

Из выражения (2.163) с учетом (2.162) можно определить пределы, в которых изменяются значения взаимной индуктивности:

0<M<VLiL2. (2.164)

Таким образом, максимальное значение взаимной индуктивности катушек не может превышать среднего геометрического их индуктивностей.

Цепи с взаимной индуктивностью при гармоническом воздействии

Для анализа цепей с взаимной индуктивностью при гармоническом воздействии можно воспользоваться рассмотренным ранее методом комплексных амплитуд. Переходя в выражениях (2.158) от мгновенных значений токов и напряжений к их комплексным изображениям и принимая во внимание, что дифференцированию гармонических функций времени соответствует умножение их изображений на /со, получаем компонентные уравнения связанных индуктивностей в комплексной форме

f/i = jwLi 4 ± /шУИ/г; Uz = /wLa 4 ± jaMl. (2.165)

Комплексное действующее значение напряжения на каждой из связанных индуктивностей помимо падения напряжения на комплексном сопротивлении индуктивности Z х, = jaL, вызванного протекающим по ней током, содержит также дополнительный член, который можно рассматривать как падение напряжения на некотором комплексном сопротивлении Z„ == jaM, называемом сопротивлением связи, вызванное протекающим по нему током другой индуктивности:

Uj =Zu Ij, ± Zm 4; u==Zl2 h ± Zm ti-

Комплексная схема замещения пары связанных индуктивностей приведена на рис. 2.44, б (другие варианты комплексных схем замещения связанных индуктивностей будут рассмотрены в следующем под-параграфе). Если индуктивной связью охвачено п индуктивностей, то комплексные действующие значения напряжений на их зажимах определяются системой уравнений

IJi = Zl\ /j ± Zm\2 4 ± •• i ZM\n in,

0 - ± Zm21 /l-}-Zi,2/2 ± ... -\-ZM2nin,

On=± Z.Mnl К ± ZMn2 2+ +ZLn /ji-

Падения напряжения на сопротивлениях связи Zmij = Zmh берут со знаком плюс при согласном включении индуктивностей и со знаком минус - при встречном.

Система уравнений электрического равновесия цепи с взаимными индуктивностями так же, как и системы основных уравнений ранее рассмотренных цепей, не содержащих взаимных индуктивностей, формируется из компонентных уравнений (уравнений ветвей), а также уравнений баланса токов и напряжений, составленных на основанин законов Кирхгофа. При произвольном внепшем воздействии соответст-кующие уравнения составляются для мгновенных значенпй токов и на-П1)яжений. при гармоническом воздействии - для их кодтлексных изображений. Напомним, что вид и количество уравиеннй, составляемых

на основании законов Кирхгофа, определяются только топологией цепи и не зависят от входящих в нее элементов. В связи с этим уравнения баланса токов и напряжений цепи, содержащей связанные индуктивности, имеют точно такой же вид, как и уравнения соответствующей цепи в отсутствие связи между индуктивностями, т. е. при М -= 0.

Пример 2.13. Составим основную систему уравнений электрического равновесия цепи, эквивалентная схема которой для мгновенных значений приведена на рис. 2.45, а.

M,3 = Mj,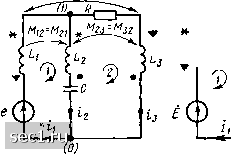

Рнс. 2.45. К примеру 2.13

На основании первого и второго законов Кирхгофа для цепи может быть составлено три независимых уравнения

В сочетании с пятью компонентными уравнениями

di., di„

42=-•n

dt " dt

dt • dt 1

получаем восемь уравнений для определения восьми нештстных величин: fj;

«а; «л: "с; "/.Г. «z.2; "ьз-