Эквивалентная схема рассматриваемой цепи для комплексных токов и напря-окений изображена на рис. 2.45, б, а основная система уравнений электрического равновесия цепи в комплексной форме имеет следующий вид:

Ol\--/wi Л-/wia ii + JioMyj /3;

= /шЛЗ! i + /ы/Из2 h + /шз h

Выражая падения напряжений на всех элементах через соответствующие токи, получаем систему из уравнений

-/1+/2Ч-/3-О;

/?/з+/й)Л1з1 /Н /to/Haj/j + ycoLa/a -/з/С/шС) /(O/Mji Ii - j&L /2 -/гз /з = 0 йля определения неизвестных токов /j, /3.

Эквивалентные преобразования участков цепей со связанными индуктивностями

Рассмотрим эквивалентные преобразования участков цепей, содержащих связанные индуктивности. В частности, покажем возможность замены их участками, не содержащими связанных индуктивностей. На -чнем с наиболее простых случаев, когда связанные индуктивности включены последовательно (рис. 2.46, а, б) или параллельна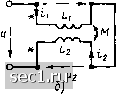

Рис. 2.46. Последовательное соединение связанных индуктивностей

(рис. 2.47, а, б). В этих случаях участок цепи, содержащий связанные индуктивности, имеет два внешних вывода, т. е. представляет собой двухполюсник. Определим его комплексное входное сопротивление и схему замещения.

При последовательном соединении связанных индуктивностей их токи равны, а напряжение на входе рассматриваемого участка цепи есть сумма напряжений на каждой из индуктивностей:

f = tl = i; « = «1 + "2- (2.166)

Ч Hz "г и и, l3 Ul и jLj -,-I I-, о-,-1 »l-. о-

Рис. 2.47. Параллельное соединение связанных индуктивностей

Используя выражения (2.166) и компонентные уравнения связанных индуктивностей (2.158), определяем зависимость между током и напряжением на зажимах рассматриваемого участка цепи:

u = {L, + L,±2M)-L.,,-

(2.167)

Как видно из выражения (2.167), участок цепи, содержащий последовательно включенные связанные индуктивности, может быть заменен эквивалентной индуктивностью (см. рис. 2.46, в)

и« - Li + Ljj ± 2М,

(2.168)

где знак плюс соответствует согласному включению, а минус - встречному. Таким образом, при согласном включении связанных индуктивностей эквивалентная индуктивность получается больше, а при встречном - меньше, чем эквивалентная индуктивность участка цепи, содержащего две последовательно включенные несвязанные индуктивности.

На использовании выражения (2.168) основан простой метод измерения взаимной индуктивности, в соответствии с которым сначала производят измерение эквивалентной индуктивности катушек при согласном Lk. согл =-1+-2 Н-+ 2М и встречном включении 1а„. встр "~ L, + - 2/W, а затем по формуле = (эк. согл - -эк- встр)/4 рассчитывают М.

При параллельном соединении связанных индуктивностей к их зажимам прикладывается одинаковое напряжение и, а входной ток рассматриваемого участка цепи складывается из токов обеих индуктивностей:

и = Ui= и,; I = «1 + i

(2.169)

Используя (2.169) и компонентные уравнения связанных индуктивностей (2.158), составляем систему уравнений

и= Li

±М

dt dt

из решения которой находим зависимость между напряжением и током на зажимах рассматриваемого участка цепи:

LLT 2М dt dt

(2.170)

В соответствии с (2.170) участок цепи, представляющий собой две параллельно включенные связанные индуктивности, обладает эквивалентной индуктивностью (рис. 2.47, в)

1э„ - (L1L2 - МУ(1, + La Т 2М),

(2.171)

причем знак минус соответствует согласному включению, а знак плюс - встречному.

При Li = Ь2== L выражение (2.171) приводится к виду

Lan - L(l - kh)f[2 (1 =F км)] = L (1 ± км)/2, откуда следует, что lim Lk == L при согласном и lim L = О при

встречном включении индуктивностей.

При коротком замыкании одной из связанных индуктивностей, например индуктивности L2 (см. рис. 2.44, а), участок цепи, содержащий связанные индуктивности, также представляет собой двухполкхник, напряжение и ток на входе которого совпадают с напряжением и током на зажимах индуктивности Lx (рис. 2.48, а). Решая систему уравнений, описывающую процессы в данном участке цепи

- dt dt

находим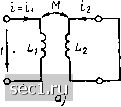

= L.„

dt dt

Рис. 2.48. Короткое замыкание одной из связанных индуктивностей

(2.172)

где LaK = (L1L2 - N1)1 - эквивалентная индуктивность участка цепи.

Таким образом, все рассмотренные идеализированные двухполюсники, содержащие связанные индуктивности, при любом воздействии могут быть заменены одной индуктивностью L La„. Комплексное сопротивление этих двухполюсников имеет чисто реактивный характер:

2 = /© LaK.

Найдем схему замещения участка цепи, содержащего две связанные индуктивности, включенные таким образом, что они имеют одну общую точку (рис. 2.49, а, б). Используя в качестве исходных компонентные уравнения связанных индуктивностей (2.158), добавим к первому из