в режиме холостого хода на зажимах / - / коэффициент передачи рассматриваемых цепей по напряжению от зажим ов 2-2 к зажимам

= 1 (3.11)

/, = 0

и не зависит от частоты внешнего воздействия. Подставляя в полученные выражения значения сопротивлений плеч делителя Zj и Z2, можно построить АЧХ и ФЧХ рассматриваемых цепей.

Определим в качестве примера комплексное входное сопротивление со стороны зажимов / - / и комплексный коэффициент передачи от зажимов }-Г к зажимам 2-2 в режиме холостого хода на выходе цепи, схема которой приведена на рис. 3.12, а. Подставляя в выражение (3.7) Zl = R, Z2 = /wL и выполняя преобразования

2ixx (/ю) = ? + /«L = VWTW е/ rce (3.12)

найдем аналитические выражения для АЧХ и ФЧХ входного сопротивления:

(«) = VR+ {Lf ; фп, ((О) = arctg (coL ?). (3.13)

Непосредственное использование выражений (3.13) для построения АЧХ и ФЧХ весьма неудобно, так как для каждой пары значений параметров R и L необходимо строить отдельную кривую. Построение существенно упрощается при замене абсолютных значений частоты ю, комплексного сопротивления Zux (/ш) и полного сопротивления Ziix(ft)) относительными (нормированными) значениями

» = u)L/.R; Znx(H=2ii,,(H/?; -Ziix(») = 2iix(M) ?. (3.14)

Из выражений (3.14) видно, что нормированная частота ш, нормированное комплексное сопротивление Zx (ую) и нормированное полное сопротивление Zn (ю) являются безразмерными величинами. С учетом (3.14) найдем выражения для нормированных АЧХ и ФЧХ входного сопротивления рассматриваемой цепи (рис. 3.13):

Znx И = К1 -f- ; Фих И = arctg ш. (3.15)

Годограф нормированного комплексного сопротивления этой цепи изображен на рис. 3.14.

Аналогичный вид имеют нормированные частотные характеристики входного сопротивления цепи, схема которой изображена на рис. 3.12, б.

Анализ полученных результатов показывает, что в области сравнительно низких частот, когда полное сопротивление индуктивности мало по сравнению с R (wL < R или ю < 1), входные сопротивления цепей (см. рис. 3.12, а, б) определяются только значением R. Сопротивление индуктивности постоянному току равно нулю, поэтому на нулевой частоте входное сопротивление цепей имеет чисто резистивный характер

it- (1)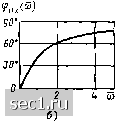

Рис. 3.13. Нормированные АЧХ (a) и ФЧХ (б) входного сопротивления цепи, схема которой приведена на рнс. 3.12, а

г J Re[z,((ju))J

Рис. 3.14. Годограф Znx(/ti))

.[Zjix (ю) = R, cpiix («) = О]. С ростом частоты модуль и аргумент входного сопротивления плавно увеличиваются, причем на достаточно высоких частотах « > 1, входное сопротивление цепи определяется только сопротивлением индуктивности [Znx (ю = оо) = ceL = оо, Фпх (со = оо) = я/2].

Рассмотрим частотные характеристики коэффициента передачи по напряжению /-Caix (/«) цепи, схема которой изображена на рис. 3.12, а. Подставляя в (3.10) Zi = R и Z = jaL, получаем

Kilx (/») =

jwL

(3.16)

R + j(aL l - iR/(aL)

Переходя в (3.16) к показательной форме записи, находим аналитические выражения для АЧХ и ФЧХ коэффициента передачи цепи по напряжению (рис. 3.15):

tix (ю) = arctg [R/iaiL)] = arcctgw.

(3.17)

Годограф комплексного коэффициента передачи цепи по напряжению изображен на рис. 3.16.

0,6 0,4 0,2 О

2 3 а)

4 со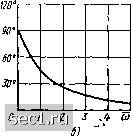

Рис. 3.15. АЧХ (о) и ФЧХ (б) коэффициента передачи по напряжению цепи, схема которой приведена на рис. 3.12, а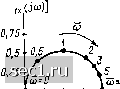

На сравнительно низких частотах (ш С 1), когда полное сопротивление индуктивности существенно меньше R, входное сопротивление цепи имеет характер, близкий к чисто резистивному, а входной ток цепи совпадает по фазе с напряжением Ui. Распределение напряжения между плечами делителя напряжения пропорционально сопротивлению этих плеч, поэтому падение напряжения на индуктивности (/ весьма мало, т. е. модуль коэффициента передачи по напряжению бли- ;т[Кг зок к нулю. Напряжение на индуктивности опережает по фазе ток индуктивности /j, а следовательно, и

входное напряжение f/j на угол, близкий к л/2. С ростом частоты сопротив-

ление индуктивности увеличивается 0,25 0,5 0,75 Re[Kz,(J(o)]

и вследствие этого распределение напряжений между плечами делителя Рис. 3.16. Годограф K2\xU<i>) изменяется. На достаточно высоких

частотах (о) > 1) практически все входное напряжение оказывается приложенным к индуктивности, поэтому модуль коэффициента передачи по напряжению /C2ix(<o) в этом случае близок к единице, а аргумент ijj.,,; (w) - к нулю.

Понятие о резонансе в электрических цепях

Амплитудно-частотные характеристики пассивных линейных цепей с одним реактивным элементом имеют вид монотонно изменяющихся кривых, поэтому амплитуда отклика таких цепей также монотонно изменяется при увеличении или уменьшении частоты внешнего воздействия. Более сложный характер имеют процессы в электрических цепях, содержащих реактивные элементы различных типов. Амплитуда отклика таких цепей может резко изменяться, когда частота внешнего воздействия достигает некоторых определенных значений. Явление резкого возрастания амплитуды отклика цепи при приближении частоты внешнего воздействия к определенному значению называется резонансом. Такое определение резонанса заимствовано из механики и справедливо только для цепей с малыми потерями. Резонанс, отвечающий этому определению, условно называется амплитуд-н ы м.

В теории цепей обычно используют другое определение резонанса, которое применяется как для цепей с малыми, так и для цепей с большими потерями. Под резонансом понимают такой режим работы электрической цепи, содержащей емкости и индуктивности, при котором реактивные составляющие входных сопротивления и проводимости Цепи равны нулю. Резонанс, отвечающий данному определению, условно называется фазовым. Можно показать, что резонансные частоты, соответствующие амплитудному и фазовому резонансам, совпадают только в идеализированном случае, когда потери в цепи равны