и переменную, изменяющуюся во времени по гармоническому закону с частотой 2(йо. Переменные составляющие энергий емкости и индуктивности находятся в противофазе так, что максимальным значениям энергии, запасаемой в емкости, соответствуют нулевые значения энергии, запасенной в индуктивности, и наоборот. Несмотря на то что WcWl являются функциями времени, суммарная энергия, запасенная в реактивных элементах цепи, постоянна:

Wsan - + = LP - const. (3.41)

Емкость и индуктивность контура при резонансе непрерывно обмениваются энергией. Обмен энергией происходит без участия источника энергии: сдвиг фаз между током и напряжением в этом режиме равен нулю, поэтому реактивная мощность,отдаваемая источником, также равна нулю, и обмена энергией между контуром и источником не происходит.

Найдем энергию, потребляемую контуром от источника за промежуток времени, равный периоду внешнего гармонического воздействия Т:

Wuidt==RPT. (3.42)

Из выражения (3.42) видно, что энергия, потребляемая контуром от источника, равна энергии, необратимо теряемой в сопротивлении потерь контура R. В идеальном случае, при отсутствии потерь в контуре (=0),энергия, потребляемая контуром от источника, равна нулю. Колебательный процесс в таком контуре будет продолжаться неограниченно долго и при отключении контура от источника (при закорачивании зажимов /-]). Таким образом, колебательный процесс в контуре без потерь должен иметь незатухаюиий характер. На практике при отключении контура от источника колебательный процесс в нем затухает, так как при каждом цикле колебаний часть электрической энергии, запасенной в контуре, необратимо преобразуется в другие виды энергии. Если контур с потерями подключить к источнику энергии, то амплитуда колебаний в установившемся режиме будет неизменной, так как потери энергии в контуре будут компенсироваться поступлением энергии от источника, и суммарная энергия, связанная с контуром, будет сохранять неизменное значение.

Найдем отношение энергии, запасаемой в реактивных элементах контура, к энергии, потребляемой контуром от источника за период Т:

WaJWn = LP/iRPT) - L/iRT).

Принимая во внимание, что при резонансе период внешнего гармонического воздействия

Т = 1 о = 2л/(йо,

получаем

WsaJW„ - w,L/(2nR) = Q/(2n),

откуда

Q = 2nW,JW„. (3.43)

Таким образом, добротность последовательного контура равна отношению энергии, запасаемой в контуре, к энергии, потребляемой им за период колебаний, умноженному на 2п. Выражение (3.43) носит общий характер и может применяться для оценки добротности колебательных систем самых различных типов (в том числе и неэлектрических).

Входные характеристики последовательного колебательного контура

При рассмотрении комплексных частотных характеристик последовательный колебательный" контур удобно представлять в виде многополюсника с тремя парами выводов (рис. 3.19, а, б). Внешнее воздействие на контур обычно задают в виде напряжения == 0, приложенного к зажимам / - /, в качестве отклика цепи рассматривают входной ток цепи tl =: ii, напряжение на емкости # или напряжение на индуктивности «з == f/g. Таким образом, последовательный колебательный контур обладает как входными, так и передаточными характе-

i Ч Г---1 k 2

С I

I 2

R I

I ij J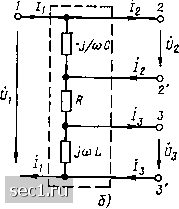

Рис. 3.19. К определению входных и передаточных характеристик последовательного колебательного контура

ристиками. В качестве входной характеристики контура будем рассматривать его комплексную входную проводимость в режиме холостого хода на зажимах 2-2 и 3-3:

K(/co) = [Fu(/«)I;,=>.=„

(3.44)

/г= /, =0

в качестве передаточных - комплексный коэффициент передачи по напряжению для случаев, когда напряжение снимается с емкости:

/<:c(/»)=[a:2i(/»)]),.>,==o=-

(3.45)

/г = /, = 0

или с индуктивности

/<l(M=[/<si(/»)]>.=>.= 0=-

/. = /3=0

Рассмотрим амплитудно-частотные и фазо-частотные характеристики входной проводимости Y (/(1)) последовательного колебательного контура:

(3.46)

y(/o)) = l/Z= 1 i? + /o)L---Lj Представляя У (/w) в показательной форме

Г(/й))К(<й)е/*() =

-/ arcfg

l ?H[wL~l/(u)C)]2

(3.47)

(3.48)

найдем аналитические выражения для АЧХ (рис. 3.20, а) и ФЧХ (рис. 3.20, б) входной проводимости:

Г(ш) =

о)С )/

/?У1+дЧш/о)о-й)о/й>)2

(3.51)

(3.49)

«((й)-arctg wL--)/ = - arctg[Q((o/Wo-(йо/(й)]. (3.50)

Для удобства приведем также амплитудно-частотные и фазо-частотные характеристики входного сопротивления контура (рис. 3.21), построенные в соответствии с выражениями:

Z (ш) = 1 /7 (со) = К1 + («/«о - «„/0)) ф (ш) = -«(м) == arctg [Q ((1)/(1)о -(1)о/(о)].

Если контур настроен на частоту источника, то мнимые составляющие входного сопротивления емкости Хс = - \/{а>,.С) и индуктивности Xl = (i>QL взаимно компенсируются, входное сопротивление контура имеет чисто резистивный характер и минимально по модулю, а полная входная проводимость У (w) достигает максимального значения и равна MR. Векторные диаграммы, соответствующие этому случаю, изображены на рис. 2.20, е. Всякое отклонение частоты внешнего воздействия от резонансной приводит к нарушению баланса между мнимыми составляющими входного сопротивления емкости и индуктивности, что в свою очередь вызывает увеличение модуля входного сопротивления Z (ю), уменьшение модуля входной проводимости У (ю) и отклонение аргумента входной проводимости (ш) от нулевого значения. Из рис. 3.20 видно, что чем выше добротность контура Q, тем более заметно выражен максимум У (со) на резонансной частоте и более резко изменяется # (ю) вблизи Wq.

При частоте внешнего воздействия со ниже резонансной мнимая составляющая входного сопротивления емкости по абсолютному значению превышает мнимую составляющую входного сопротивления индук-