тивности ( jjcc I > Xl) и входное сопротивление контура имеет резистив-но-емкостный характер (-я/2 < ср < 0). В пределе, при со = О, входное сопротивление контура будет иметь чисто емкостной характер (ф =: - я/2), полное сопротивление контура Z (со) бесконечно велико, а модуль входной проводимости Y (ш) равен нулю. Векторные диаграммы для (1) < (йо и \хс\> Хь приведены на рис. 2.20, г.

На частоте выше резонансной (со > coq) мнимая составляющая входного сопротивления емкости по абсолютному значению меньше, чем мнимая составляющая входного сопротивления индуктивности (л:с1<С <: jcjj, входное сопротивление контура имеет резистивно-индуктив-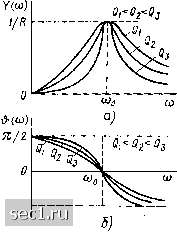

-7i/z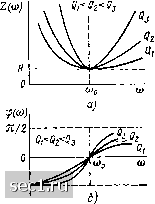

Рис. 3.20. АЧХ (а) и ФЧХ (б) входной проводимости последовательного колебательного контура

Рис. 3.21. АЧХ (а) и ФЧХ (б) входного сопротивления последовательного колебательного контура

НЫЙ характер (О < ф < л/2). С увеличением частоты аргумент входного сопротивления контура ф (w) будет стремиться к п/2 (аргумент входной проводимости & (со) будет стремиться к - л/2), модуль входного сопротивления контура Z (ю) неограниченно возрастать, а модуль входной проводимости У (ш) - стремиться к нулю.

Комплексные частотные характеристики входной проводимости Y (/(1)), приведенные на рис. 3.20, имеют чисто качественный характер и неудобны для практического использования, так как содержат большое число параметров, причем для каждого сочетания R, Q я (и, необходимо строить отдельные кривые. Поэтому на практике обычно применяют нормированные входные характеристики, которые позволяют в обобщенной форме построить кривые для всех возможных сочетаний значений параметров. В качестве аргумента нормированных характеристик удобно использовать так называемую обобщенную расстройку, которая определяется выражением

L со„

(3.52)

На резонансной частоте = О, на частотах ниже резонансной <0, причем нулевому значению ю соответствует 1 = - оо. На частотах выше резонансной g> О, а при ю =. оо значение обобщенной расстройки также равно бесконечности. В ряде случаев в качестве аргумента нормированных частотных характеристик удобно использовать а б с о-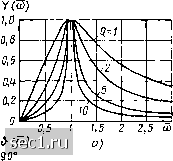

60 30°

30° -60° -90°

~8 -6 -Ч-2-1 О I 2 Ц- 6 £,

Рис. 3.22. Нормированные АЧХ (а) и ФЧХ (б) входной проводимости последовательного колебательного контура

Рис. 3.23. Обобщенные АЧХ (а) и ФЧХ (б) входной проводимости последовательного колебательного контура

лютную расстройку Асо = ю - ©о, относительную расстройку б А(й/(1)о = (ю - ©(Уюо или нор м и -рованную частоту ю - ю/соо.

Комплексная входная проводимость Y (/ю) и ее модуль Y {<л) обычно нормируются по значению, которое они принимают на резонансной частоте [У (ушс) Y (юс) =

Г(/со) = У (/со)/У 0"«о) - RY (/со); У (со) - У (©)/У (щ) - RY (й). (3.53)

С использованием (3.52), (3.53) выражения (3.47), (3.49) (3.50) преобразуются к виду

У(со)==

Y{i<o).Y{jl)

:У()е/*Ш .1/(1 +Л);

й (со) = - arctg [Q ((b/wi - (Bu/(o)J = •& () =-- arctg

(3.54)

/w[y(j£,)]

Нормированные амплитудно-частотные и фазо-частотные характеристики входной проводимости последовательного колебательного контура приведены на рис. 3.22 и 3.23 (в последнем случае комплексные частотные характеристики цепи называют обобщенными). Годограф нормированной комплексной входной проводимости последовательного колебательного контура У (Ц) имеет вид окружности (рис. 3.24).

Используя входные характеристики, найдем зависимость входного контура от частоты. Пусть к зажимам контура

(см. рис. 3.17, в) подключен идеальный источник напряжения e(t) фЕ=Ее, частота которого может изменяться в широких пределах, а действующее значение Е и начальная фаза ipe - постоянны. Комплексный ток контура /] определяется произведением комплексной входной проводимости контура на комплексное действующее значение э. д. с;

л = Г (/(о) £ = К (и) е/« Еее = eY (со) е - а е*.. (3.55)

Из выражения (3.55) находим действующее значение входного тока контура и его начальную фазу как функции круговой частоты ю:

-0,5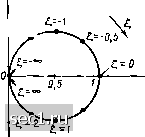

= 0,5

Рис. 3.24. Годограф нормированной комплексной проводимости последовательного колебательного контура

/, = £У(ш)

/? Vl+[Q (o)/u)„-(oo/u))f грг = (со) -f ij) = ij) - arctg [Q (<о/щ -

- (йо/©)).

Нормируя ток /i, по его максимальному значению /о = e/r, которое достигается, когда ю = юв, и переходя от круговой частоты а> к обобщенной расстройке , окончательно получаем

Л =/, о = F (сй) = F (Ю = I Н--arctg t

(3.56)

Таким образом, зависимость нормированного входного тот контура 11 от частоты совпадает с нормированной амплитудно-частотной характеристикой входной проводимости контура, а зависимость начальной фазы \1;>1 от частоты совпадает с нормированной фазо-частотной характеристикой контура, смешанной на ijg.