Передаточные характеристики последовательного колебательного контура

Найдем коэффициент передачи контура по напряжению Кс Ц<) для случая, когда напряжение снимают с емкости (см. рис. 3.19). При холостом ходе на зажимах 2-2 и 3 - 3 через все элементы контура протекает один и тот же ток h = Y (/со) Ui, где У (/со) - комплексная входная проводимость контура, определяемая выражениями

(3.47) и (3.48). Выходное напряжение контура

:й) U.,ZcIi= -jy{MUj{4iC). (3.57) (со;

Поставляя (3.57) в (3.45), находим выражение для коэффициента передачи контура по напряжению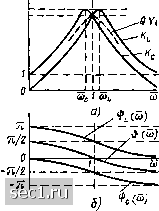

Кс(/(о) =

и = /,=0

= -1-~У{Н.

Рис. 3.25. АЧХ (а) и ФЧХ (б) коэффициента передачи по напряжению последовательного колебательного контура

(3.58)

Умножая числитель и знаменатель (3.58) на (Оо и используя соотношения (3.34), (3.53), преобразуем (3.58) к виду

А:с(/со)-/<с(со)е*<> = = qJ у(ш)е/[««»-"/2],

откуда можно определить модуль (рис. 3.25, а) и аргумент (рис. 3.25, б) комплексного коэффициента передачи цепи по напряжению:

Кс (ю) = MoQ? (w)/m; ijic (w) •& (со) - я/2. (3.59)

Здесь У (со) ий (со) - нормированные АЧХ и ФЧХ входной проводимости последовательного колебательного контура, определяемые выражениями (3.54).

Используя аналогичный подход, находим модуль (рис. 3.25, а) и аргумент (рис. 3.25, б) комплексного коэффициента передачи цепи по напряжению

A:L(/0))--=/<:L(»)e*b<);

для случая, когда напряжение снимают с индуктивности,

Kl (м) = QcoT (m)/(Oo; (w) = •& (со) -f я/2. (3.60)

Как следует из определения добротности, на резонансной частоте (со = (йц) действующее значение напряжения на емкости равно действующему значению напряжения на индуктивности и в Q раз превышает напряжение на входе контура, поэтому Кь («о) = Кс(юо)=

= Q. При (й = О сопротивление емкости бесконечно велико, напряжение на емкости 0 = Ui, напряжение на индуктивности равно нулю. Поэтому Кь (ш = 0) = О, /Сс (ю = 0) = 1- На высоких частотах ю = оо сопротивление индуктивности бесконечно велико, поэтому напряжение Ui оказывается практически полностью приложенным к индуктивности, а напряжение на емкости равно нулю. Таким образом, /С, ((1) = оо) = 1, (а = оо) = 0.

Максимум зависимости Кс («) соответствует частоте, несколько более низкой, а максимум Kl (со) - частоте, несколько более высокой, чем резонансная. Однако эти смещения максимумов /Сс (м) и Кь (ю) относительно резонансной частоты очень малы и на практике ими всегда можно пренебречь. Действительно, исследуя кривые /Сс (ю) и Kl («) на экстремум, легко установить, что функция Кс («) имеет максимум на частоте

а)с=»оКТ=Т7да, (3.61)

а функция Kl (<«>) - на частоте

Подставляя (3.61) и (3.62) соответственно в выражения (3.59) и (3.60), находим, что максимальные значения обеих функций одинаковы:

/<:z.(C0Z.)=/<:c(C0C)=-qj/ 1-==Кт.. (3.63)

Рассматривая выражения (3.61)-(3.63), нетрудно прийти к заключению, что при Q > 5 отличие юх, и со с от «о не превышает 0,01 (1)о, а /Стах - Q < 0,005Q, поэтому во всех практически важных случаях можно считать, что Кь (w) и /(с (ю) имеют максимум на резонансной частоте, причем Ктах - Q-

На рис. 3.25, а, который носит чисто качественный характер, смещение кривых Кь (ю) и Кс (м) относительно друг друга преувеличено с тем, чтобы показать, что максимумы кривых Кь (ю) и /<с («) находятся на разных частотах. В действительности в узком диапазоне частот, близких к резонансной, когда можно положить ю/мо » 1, эти зависимости почти совпадают друг с другом и с зависимостью

QY (<й), т. е. Кь («) » Кс Н QY («).

Если к входу последовательного колебательного контура подключить источник напряжения е (t) = Ё = fe*, частота ю которого изменяется в широких пределах, а действующее значение э. д. с. Ё и начальная фаза % сохраняют неизменное значение, то зависимость нормированного выходного напряжения U от частоты будет совпадать с нормированной АЧХ входной проводимости контура:

и = UKEQ) - U,/{EQ) -= Y (»).

Напомним, что такой же вид имеет зависимость нормированного входного тока контура /i от частоты (3.56).

Таким образом, нормированную входную проводимость контура Y (ш) можно рассматривать как нормированную реакцию последовательного колебательного контура на воздействие в виде источника э. д. с. с изменяющейся частотой и неизменной амплитудой в режиме холостого хода на зажимах 2-2 и 3-3.

Избирательные свойства последовательного колебательного контура

Н(ш)

0,707

<

Важнейшая особенность последовательного колебательного контура заключается в том, что амплитуда реакции контура на гармоническое воздействие существенно зависит от частоты. На резонансной частоте и в узком диапазоне частот около нее амплитуда отклика достигает наибольшего значения; на частотах, значительно отличающихся от резонансной, амплитуда отклика во много раз меньше максимального значения. Если на вход такого контура подать сумму гармонических колебаний различных частот, имеющих одинаковую амплитуду, то на выходе можно обнаружить, что амплитуда колебаний, частота которых близка к резонансной, значительно превышает амплитуду колебаний, частота которых отличается от резонансной. Контур

как бы «пропускает» колебания одних частот и «не пропускает» колебания других частот. Способность электрической цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.

В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой пропускания цепи, и быть равным нулю за пределами этого диапазона. Нормированная АЧХ идеальной избирательной цепи должна иметь прямоугольную форму (рис. 3.26, кривая /). АЧХ реальных избирательных цепей, в том числе и АЧХ последовательного колебательного контура, отличаются от характеристик идеальной избирательной цепи (рис. 3.26, кривая ) отсутствием резкой границы между диапазонами пропускаемых и задерживаемых (подавляемых) частот. Очевидно, избирательные свойства реальных цепей будут тем выше, чем ближе к прямоугольной будет форма их нормированной

Полоса пропускания реальных избирательных устройств условно определяется как диапазон частот, в пределах которого амплитуда отклика цепи не падает ниже уровня MY2 = 0,707 от максимального значения. На частотах, соответствующих границам полосы пропускания, амплитуда отклика составляет MY2 от максимального значения, а потребляемая цепью активная мощност] Рл = = PR в 2 раза меньше максимальной.

н

Рис. 3.26. Нормированные АЧХ избирательной цепи:

/ - идеальной; - реальной