Избирательные свойства последовательного колебательного контура определяются формой нормированной АЧХ входной проводимости контура Y (ю). На резонансной частоте нормированная входная проводимость контура равна единице. Определим значения обобщенной расстройки и угловой частоты Юрр, соответствующие границам полосы пропускания контура. Полагая в выражении (3.54) I = gp, Y а,р) = 1/2, получим \/Vl + Up = I/V2, откуда = ,pi =

Меньшее значение обобщенной расстройки = -1 соответствует нижней границе полосы пропускания, большее = 1 - верхней. Из выражений (3.54) следует, что на границах полосы пропускания аргумент входной проводимости контура равен ±л/4 (см. рис. 3.23, б), а реактивная составляющая входного сопротивления х = = coL- 1/((йС) равна по абсолютному значению сопротивлению потерь контура R.

Полагая в выражении (3.52) g = -1, (й=(й„и g = 1, » = Юв, запишем систему уравнений для определения нижней »„ = wpi и верхней «в =- Юррз граничных частот:

(3.64) (3.65)

Решая (3.64), найдем

Сй„=(1)„

(J/2)-fKl+dV4];

«„=«o[(-d/2)4- VT+dFJl

где d - l/Q - затухание контура.

Ширина полосы пропускания пропорциональна резонансной частоте контура

2А(йо = а>в - Мн = 4>cd - (nJQ, (3.66)

а относительная ширина полосы пропускания

2А(йо/©о = 1/Q = d (3.67)

равна его затуханию.

Таким образом, избирательные свойства последовательного колебательного контура зависят от его добротности: чем выше добротность контура, тем меньше ширина полосы пропускания (см. рнс. 3.22, а).

В связи с тем что Y (сй) - это нормированный отклик цепи в режиме холостого хода на зажимах 2-2 и 3-3 на внешнее гармоническое воздействие, задаваемое источником напряжения, подключенным к зажимам /-/, из выражений (3.65)-(3.67) можно определить избирательность колебательного контура только в случае, когда внутреннее сопротивление источника энергии равно нулю, а входное сопротивление нагрузки, подключенной к зажимам 2-2 или 3-3, бесконечно велико. Рассмотрим влияние внутреннего сопротивления источника энергии и сопротивления нагрузки на избирательные свойства последовательного колебательного контура.

Пусть контур питается от источника энергии с конечным внутренним сопротивлением Ri (рис. 3.27, а). Очевидно, что включенные последовательно сопротивления Rt я R можно заменить сопротивлением RsK Ri + R. При этом рассматриваемая схема преобразуется в схему, приведенную на рис. 3.17, в, и может быть описана соотношениями, полученными на основании анализа этой схемы при замене R на RsK-

В частности, добротность такого контура определяется выражением

= Q (3-68)

где Q - pIR - добротность контура без учета сопротивления источника.

Ширина полосы пропускания контура с учетом внутреннего сопротивления источника энергии может быть найдена из выражения (3.66) при замене Q на Qa„i: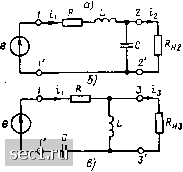

Рис. 3.27. К учету влияния внутреннего сопротивления источника н сопротивления нагрузки на избирательные свойства последовательного колебательного контура

(3.69)

Как видно из выражений (3.68), (3.69), наличие внутреннего сопротивления источника энергии уменьшает эквивалентную добротность контура и снижает его избирательность. Поэтому с целью повышения избирательных свойств контура желательно, чтобы источник энергии, к которому, подключен контур, имел как можно меньшее внутреннее сопротивление, т. е. по свойствам приближался к идеальному источнику напряжения.

Пусть к зажимам 2-2 или 3-3 последовательного колебательного контура подключено сопротивление нагрузки (рис. 3.17, б, в) так, что ток /а или /3 не равен нулю. Очевидно, что сопротивление нагрузки, подключенное параллельно емкости или индуктивности, влияет на работу контура таким же образом, как сопротивления /?спар и Rbaap, входящие в параллельные схемы замещения конденсатора и индуктивной катушки. Ранее отмечалось, что параллельные схемы замещения элементов могут быть заменены последовательными, причем при высокой добротности элементов Спар » Споо С, Lnap «J

Ljioc,~L, а сопротивления Rcaoc и ьпос обратно пропорциональны сопротивлениям/? с пар (3.23) и Rtnap (3.21). Таким образом, сопротивление нагрузки R„2, подключенное параллельно емкости, и /?н8. подключенное параллельно индуктивности, могут быть заменены последовательно включенными сопротивлениями

R;,2 « 1/(0) С* /?„2); RL3» LVR.

влияние нагрузки на контур сопро-Если i?„2 = R„3 = Rh, то на ча-(!)(,), внесенные в контур сопро-

(3.70)

Сопротивления Rk2 и Ra, учитывающие работу контура, назовем внесенными тивлениями нагрузки

стотах, близких к резонансной (ю тивления нагрузок

RL2» RU « pVR„ « R«.

Влияние i?H на параметры контура аналогично влиянию внутреннего сопротивления источника Ri, т. е. с увеличением R снижается эквивалентная добротность контура и ухудшается его избирательность. Используя (3.70), найдем выражения для эквивалентной добротности контура и ширины полосы пропускания:

О - Р О

Чак2

2А(йо =

(3.71)

Из выражений (3.71) следует, что для увеличения эквивалентной добротности контура и улучшения его избирательности необходимо, чтобы сопротивление нагрузки контура R„ было бы как можно большим, т. е. чтобы на зажимах 2-2 и 3-3 был обеспечен режим работы, близкий к режиму холостого хода.

§ 3.3. ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР

Виды параллельных колебательных контуров. Схемы замещения

Параллельным колебательным контуром называется электрическая цепь, в которой индуктивные катушки и конденсаторы размещены в двух ветвях, подключенных параллельно источнику энергии. Принципиальные электрические схемы параллельных колебательных контуров различных видов приведены на рис. 3.28.

В простейшем случае параллельный колебательный контур содержит индуктивную катушку в одной из параллельных ветвей, а конденсатор - в другой (рис. 3.28, а). Такой контур называется параллельным колебательным контуром 1-го (о с н о в н о г о) вида. Параллельный колебательный контур 2-го (с неполным включени-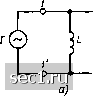

= =С 0 Г (5==Tl

-1 L o i-1 1-п- I-

Рис. 3.28. Принципиальные электрические схемы параллельных колебательных контуров: а - основного вида; б - второго вида; в - третьего вида