входного сопротивления параллельного колебательного контура второго вида

а на частотах выше частоты резонанса напряжений - резистивно-индуктивный. На частоте резонанса напряжений входное сопротивление контура имеет чисто резистивный характер и достигает минимального значения, определяемого сопротивлением потерь второй ветви.

Покажем, что добротность парал- 2(w) лельного колебательного контура с неполным включением индуктивности не зависит от коэффициента включения и равна добротности последовательного колебательного контура, составленного из тех же элементов. Пусть контур настроен на частоту источника сигнала, а напряжение и ток на входе контура определяются соотношениями

1=УТ 1 cos К 0;

M = j/Tf/oC04((Oo 0 =

= K2/?o(pO/oCosK0- (3.93) Токи ветвей контура ii и /а на резонансной частоте имеют одинаковые действующие значения

Ло = /20 » VJiLi) (3.94)

и отличаются по фазе на угол л, а напряжение на емкости Uc отстает по фазе от тока второй ветви на угол л/2:

1\ - К т /ю cos (©„/ - л/2) - /ю sin ((й„ о;

h=VT /20 cos {щ1 + я/2) = ~V~ ho sin (юо ty, Uc = V~2 cos (wo 0/(Mo C) = K"2" p /10cos (wo 0-Определим энергию, запасаемую реактивными элементами контура: = (Liif/2) + (L2t/2) + {СиЫ2) = (Li + /.2) /f о sin (№„ О +

+ CpVfoCos2(cD„0 = J/fo, (3.95)

и энергию, потребляемую контуром за период Т:

W„ - (/?! /Ь + /?2 /20) Г = (/?! + i?,) /?о Г = о г. (3.96)

Подставляя (3.95) и (3.96) в (3.43), получим выражение для добротности параллельного колебательного контура с неполным включением индуктивности:

Q = 2nWjW„ = 2nU{RT) = UR - p/R, (3.97)

которое совпадает с выражением для добротности параллельного контура основного типа и соответственно с выражением для добротности последовательного колебательного контура, построенного из тех же элементов. Далее, используя (3.93), (3.94) и (3.97), найдем, что

на резонансной частоте действующие значен и я токов ветвей контур; превышают действующее значение входного тока контура в pQ раз

/10 0 = IJh = Ro (PlVM,) = pplL/{RLL,) = PlQ.

Итак, важнейшие параметры параллельного колебательного контура 2-го вида (частота резонанса токов, характеристическое сопротивление и добротность) не зависят от коэффициента включения индуктивности р. В то же время резонансное сопротивление контура является функцией р.

Указанная особенность параллельного колебательного контура широко используется на практике при согласовании его с источником энергии. Согласование осуществляют путем надлежащего выбора значения коэффициента включения, причем при изменении р настройка контура и ширина его полосы пропускания, определяемая эффективной добротностью, не изменяются.

Наличие ярко выраженного минимума в АЧХ контура с неполным включением индуктивности может быть использовано для подавления колебаний, частота которых близка к Шрн рассматриваемого контура.

Параллельный колебательный контур третьего вида

Колебательный контур этого типа по своим свойствам в значительной степени подобен параллельному колебательному контуру второго вида. Используя эквивалентную схему контура, приведенную на рис. 3.35, нетрудно показать, что частота резонанса токов Юрт, характеристическое сопротивление р и добротность Q параллельного колебательного контура с неполным включением емкости совпадают с резонансной частотой, характеристическим сопротивлением и добротностью последовательного колебательного контура, построенного из тех же элежнтов и, следовательно, обладающего теми же суммарной емкостью С --- CiCJ{Ci + С) и суммарным сопротивлением R Ry+ R-

Частота резонанса напряжений Шрц рассматриваемого контура определяется параметрами элементов второй ветви

= 1 /VLQ - too V CIC2 =сОо к1 -Рс

и зависит от коэффициента включения емкости

Рс- С 1С, CJ{C, + С).

Резонансное сопротивление контура с неполным включением емкости так же, как и резонансное сопротивление контура с неполным включением индуктивности, пропорционально квадрату коэффициента включения

Ro (Рс) pYc/R " RoPc.

Здесь Ro = p/R - резонансное сопротивление параллельного контура основного вида, обладающего той же индуктивностью L, суммарной емкостью С и суммарными сопротивлением R, что и рассматриваемый контур

АЧХ и ФЧХ входного сопротивления параллельного колебательного контура с неполным включением емкости приведены на рис. 3.36. у{а частотах ниже Юрн входное сопротивление обеих ветвей контура имеет резистивно-емкостной характер; на частоте резонанса напря-5кений входное сопротивление контура имеет чисто резистивный характер и достигает минимального значения, определяемого в основном сопротивлением потерь второй ветви; на частотах (йр„ < ю <: входное сопротивление контура имеет резистивно-индуктивный характер; при (1) = Юрт входное сопротивление контура имеет чисто резистив-

) ъ -о-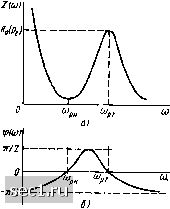

Рис. 3.35. Эквивалентная схема параллельного колебательного контура третьего вида

Рис. 3.36. АЧХ (а) и ФЧХ (б) входного сопротивления параллельного колебательного контура третьего вида

НЫЙ характер и его модуль достигает максимального значения Rq (рс); на частотах выше частоты резонанса токов входное сопротивление контура определяется в основном параметрами первой ветви и имеет резистивно-емкостной характер.

§ 3.4. СВЯЗАННЫЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ Общие представления о связанных контурах

Два контура-электрической цепи называются связанными, если возбуждение колебаний в одном из них приводит к возникновению колебаний в другом. Каждый из связанных контуров может быть либо колебательным (если он содержит индуктивные катушки и конденсаторы), либо апериодическим (если он содержит реактивные элементы только одного типа). Наибольший практический интерес представляют связанные колебательные контуры, так как их избирательные свойства лучше, чем избирательные свойства одиночных колебательных контуров.

В зависимости от типа элемента, через который осуществляется взаимодействие между контурами, различают контуры с трансформаторной, индуктивной, емкостной и комбинированной (индуктивно-емкостной) связями. По Способу включения элемента связи связанные контуры подразделяют-