что соответствует настройке на частоту источника контура, эквивалентного вторичному. Действующее значение тока вторичного контура в этом случае

/ 2 max - • -rr- --:

Настройку связанных контуров на первый или второй частные ре-зонансы обычно выполняют только в тех случаях, когда конструкция устройства позволяет производить изменение параметров реактивных элементов только одного из контуров. Если можно изменять параметры реактивных элеменов, входящих в разные контуры, при фиксированном значении сопротивления связи, то производят настройку контуров на индивидуальный резонанс. Параметры реактивных элементов в этом случае выбирают так, чтобы обеспечить равенство нулю мнимой составляющей собственного сопротивления каждого из контуров при разомкнутом другом контуре:

- л:,., - 0. (3.120)

Из выражений (З.П5) видно, что выполнение условия (3,120) обеспечивает равенство нулю мнимых составляющих сопротивлений, вносимых в каждый из контуров:

вна - в„2 0. (3.121)

Таким образом, при настройке связанных колебательных контуров иа индивидуальный резонанс одновременно выполняются условия настройки контуров на первый и второй частные резонансы (3.118), (3.119).

Подставляя (3.120), (3.121) в выражение (3.117), найдем действующее значение тока вторичного контура при настройке на индивидуальный резонанс:

/U), . U,.i£. 3 ,22)

Настройка связанных контуров на первый и второй частные или на индивидуальный резонансы позволяет получить максимальное значение тока вторичного контура, соответствующее некоторому заданному значению сопротивления связи, однако не позволяет достигнуть наибольшего возможного (максимум максиморум) значения тока J.i

Если настройка связанных контуров на первый или второй частные резонансы сопровождается последующим выбором оптимального сопротивления связи, то говорят о настройке контуров на сложный резонанс. Определим оптимальное сопротивление связи при сложном резонансе x\Wpt, соответствующее случаю, когда связанные контуры предварительно настроены на первый частный резонанс. Приравнивая нулю первую производную по \Xi\ тока вторичного контура, настроенного на первый частный резонанс, получаем

/гшах Гц f xl г ri/(rl t+xU)-2xli rJ{rl, + ж I,)

откуда

riiirh + xh)-xhr22 = 0. (3.123)

Решая уравнение (3.12.3), находим оптимальное сопротивление связи

I ;lVopf I = Virh + xh) гп/гп (3-124)

и соответствуюш,ее ему действующее значение тока вторичного контура

/гтах max - ЕА2УгггГ2г)- (3.125)

Если связанные контуры были предварительно Настроены на второй частный резонанс, то оптимальное сопротивление связи IxiVoptl и действующее значение тока вторичного контура /дах max при настройке на сложный резонанс определяются выражениями:

\x\Vopt\=V{r\i+xh)rJrii; (3.126)

/гтахтах = £i/(2 У /"22) =/2 max max = 2 щах max- (3.127)

Итак, наибольшее возможное значение тока вторичного контура при настройке на сложный резонанс не зависит от того, какой из контуров был предварительно настроен иа частный резонанс.

Наибольший практический интерес представляет настройка связанных колебательных контуров на полный резонанс, которая выполняется в два этапа: на первом этапе связанные контуры настраивают на индивидуальный резонанс, а затем выбирают оптимальное сопротивление связи между ними. Анализируя выражение (3.122), найдем IxiVoptI и действующее значение тока вторичного контура, соответствующие настройке контура на полный резонанс:

Ui2UI = Kb; (3.128)

i?L. шах = £i/(2 КГ) = /2 ,„ах „,ах (3.1 29)

Из выражений (3.124)-(3.129) следует, что как при настройке на сложный резонанс, так и при настройке на полный резонанс во вторичном контуре достигается одно и то же значение тока /гтах max, однако в последнем случае это имеет место при меньшем значении сопротивления связи.

Зависимость тока вторичного контура от абсолютного значения сопротивления связи при настройке на полный или сложный резонан-сы иллюстрируется кривыми, приведенными на рис. 3.41, в. Как следует из выражений (3.110), (3.115), с ростом сопротивления связи э. д. с, вносимая во вторичный контур, возрастает по линейному закону (рис. 3.41, а), а вещественная составляющая вносимого во вто-)ичный контур сопротивления - по квадратичному (рнс. 3.41,6). Лри сопротивлении связи, меньшем оптимального, суммарное сопротивление вторичного контура + Гвн2 определяется в основном собственным сопротивлением вторичного контура гч, поэтому с ростом

7* * ,95 -

сопротивления связи происходит увеличение тока вторичного контура (рис. 3.41, в). При сопротивлении связи, большем оптимального, суммарное сопротивление вторичного контура определяется в основном сопротивлением, вносимым во вторичный контур Гвнг. которое с увеличением {xnl растет быстрее, чем вносимая в контур э. д. с. Вследствие этого при сопротивлении связи, большем A:i2optl. дальнейший

рост \хц\ приводит к уменьшению тока вторичного контура.

Найдем значение коэффициента связи между контурами cBopt, соответствующее настройке контуров на полный резонанс. Анализ выражений (3.101) и (3.103) показывает, что для контуров с, внутренней емкостной и индуктивной связями коэффициент связи между контурами равен отношению сопротивления связи к среднему геометрическому реактивных сопротивлений того же типа обоих контуров. Если связанные контуры настроены на индивидуальный резонанс, то с учетом (3.120) сопротивление емкостных элементов каждого из них равно по абсолютному значению сопротивлению индуктивных элементов и приблизительно равно характеристическому сопротивлению контура. Таким образом, для контуров с внутренней емкостной и индуктивной связями можно записать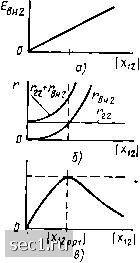

max г max max

Рис. 3.41. Зависимость вносимой э. д. с. (а), резистивной составляющей вносимого сопротивления, суммарного сопротивления (б) и тока (в) вторичного контура от сопротивления связи

разовав их в эквивалентные стройке связанных контуров вид

cB = UiJ/Kpip2- (3.130)

Выражение (3.130) можно использовать и при расчетах связанных контуров других типов, предварительно преоб-контуры с внутренней связью. При на-на полный резонанс (3.130) принимает

*св opt = ii2opt \/V PlР2 = К г,rjip, рг) = 1 /VQiQ2=V dd.

Если первичный и вторичный контуры имеют одинаковую добротность Qi = = Q - l/d, то оптимальный коэффициент связи между контурами, соответствующий настройке на полный резонанс, равен затуханию контура d:

Йсвор. = 1/Q = (3.131)

Величина

А = QcB (3.132)

получила название параметра связи. Как видно из выражения (3.131), при настройке связанных контуров на полный резонанс А = 1.