Частотные характеристики связанных контуров

Рассмотрим зависимость тока вторичного контура от частоты для случая, когда параметры обоих контуров одинаковы: .

Хц = xi = х; Гц = = >", «01 = = а>о\ Pi = Рг = Р; Qi = Q2 = Q-Собственные сопротивления первичного и вторичного контуров в этом случае могут быть представлены в следующей форме:

£ii = 222 = - + /jc = r(l + /1), (3.133)

где I = х/г - обобщенная расстройка.

Подставляя (3.113), (3.133) в (3.108), найдем выражения для комплексного действующего значения

и действующего значения

V[l-i+(i2/-)T+4 2r

тока вторичного контура. Принимая во внимание, 4To£i/(2r) есть наибольшее возможное значение тока вторичного контура

, h шах п,ах -1/(2 К") = £l/(2r),

а 1x121/ с учетом соотношений (3.130) и (3.132) приблизительно равно параметру связи

\хм\1г = д:,2 р/(р-) ~ KbQ =- А, выражение (3.134) можно записать в более компактной форме

4 = 2Л/2 ,„ах ,„ах/К (1 -+ Af + 42. (3.135)

Очевидно, что экстремумы функции /2 = /2 {\) совпадают с экстремумами знаменателя выражения (3.135). Приравнивая нулю первую производную знаменателя по получим -4 (1 - -f Л) +

+ 8g == О или

1 (g+ 1 - Л) = 0. (3.136)

Уравнение (3.136) имеет три решения:

Первое из них соответствует случаю, когда со = »„. Второе и третье решения имеют физический смысл только при - 1 > О, т. е. когда параметр связи не меньше некоторого критического значения кр = 1.

Таким образом, при больших значениях параметра связи {А > Л„р) функция /2 = /2 () имеет три экстремума, а при малых значениях параметра связи (А < Л„р) - один. При А = Ар все три решения уравнения (3.136) совпадают и функция /2= /а (1) имеет один экстре-

мум. Отметим, что критическое значение параметра связи соответствует оптимальной связи между контурами при настройке на полный резонанс.

Зависимость нормированного тока вторичного контура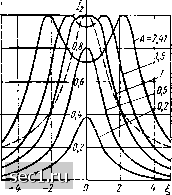

h = hlh ,„ах шах = 2Л/К( 1 - + A-f 4 Р

ОТ обобщенной расстройки показана на рис. 3.42. При слабой связи между контурами (Л < Л„р) частотные характеристики /а имеют вид «одногорбых» кривых, причем максимальное значение тока вторичного контура, достигаемое на резонансной частоте = 0), меньше, чем 2 max ша\- с увеличением параметра связи вплоть до Л Лкр -= 1 значения тока /г в максимуме увеличиваются, а кривые остаются «одногорбыми». При Л = = Лкр ток вторичного контура на резонансной частоте (=-0) равен /а max max-

При дальнейшем увеличении связи между контурами ток вторичного контура на резонансной частоте {\ = 0) начнет уменьшаться и частотные характеристики /г приобретут вид «двугорбых» кривых. Максимальное значение тока 1 = =- /2 тач шах Достигается на частотах связи, соответствующих обобщенным расстройкам g = ±YА- 1. Физически существование максимумов тока /2 на частотах связи объясняется тем, что на них реактивная составляющая тура собственного сопротивления каждого из

контуров компенсируется реактивной составляющей вносимого сопротивления. С увеличением параметра связи Л при сильной связи между контурами (Л > Лр) максимальное значение тока вторичного контура, достигаемое на частотах связи, остается равным /-2 max тахрасстояние между максимумами увеличивается, а значение тока /2 на резонансной частоте - 0) в соответствии с кривой, изображенной на рис. 3.41, б, уменьшается. При

Л > 2,41 значение 1 на резонансной частоте упадет ниже 0,707/2max max. при ЭТОМ полоса пропускания связанных контуров распадется на два участка.

По сравнению с одиночными колебательными контурами связанные контуры обладают существенно лучшими избирательными свойствами, форма их нормированных АЧХ намного ближе к прямоугольной и имеет большую крутизну склонов на границах полосы пропускания.

Дополнительное удобство состоит в возможности плавно изменять ширину полосы пропускания за счет изменения коэффииента связи между контурами. Это обусловило широкое применение связанных контуров в различных радиотехнических устройствах.

Рнс 3 42. Зависимость нормированного тока вторичного контура от обобщенной расстройки при различных значениях параметра связи: пунктир - частотная характеристика одиночного колебательного кои-

Анализ линейных

электрических цепей

с постоянными

параметрами

при гармоническом

воздействии

§ 4.1. МЕТОДЫ ФОРМИРОВАНИЯ УРАВНЕНИЙ ЭЛЕКТРИЧЕСКОГО РАВНОВЕСИЯ ЦЕПИ

Общие представления о методах формирования уравнений электрического равновесия сложных цепей

До сих пор рассматривались только простейшие, одноконтурные и двухузловые цепи, а также цепи, которые приводятся к простейшим с помощью элементарных преобразований. Для анализа таких цепей использовалась основная система уравнений электрического равновесия, включающая в себя р - рит - Рпп компонентных и р топологических уравнений, составленных на основании законов Кирхгофа. С помощью основной системы уравнений электрического равновесия, в принципе, можно производить анализ и сложных цепей, однако с ростом числа ветвей цепи анализ усложняется, так как для определения токов и напряжений цепи, содержащей р ветвей, приходится решать систему из 2р - рин - Рт уравнений. Число одновременно решаемых уравнений может быть уменьшено, если учесть, что не все 2/0 - Рин - Pat неизвестных токов и напряжений ветвей являются независимыми.

Для каждой электрической цепи можно выделить совокупность независимых токов и (или) напряжений ветвей, зная которые, .можно определить все остальные (зависимые) токи и напряжения. Значения независимых токов и напряжений находят путем решения сокращенной системы уравнений электрического равновесия, содержащей меньшее, чем 2р - /?ин - Pai, число уравнений. В связи с тем что выбор независимых токов и напряжений неоднозначен, а число независимых токов и напряжений определяется тем, какие именно величины выбраны в качестве независимых, трудоемкость анализа цепи определяется рациональностью выбора системы независимых токов и напряжений.