Методы, основанные на непосредственном применении законов Кирхгофа

К методам формирования уравнений электрического равновесия цепей, основанным на непосредственном применении законов Кирхгофа, относятся метод токов ветвей и метод напряжений ветвей. В методе токов ветвей в качестве независимых переменных, относительно которых составляется сокращенная система уравнений электрического равновесия, используют токи ветвей исследуемой цепи. Этот метод основан на том, что ток и напряжение каждой ветви, за исключением ветвей, содержащих идеализированные источники тока, а также ветвей, составленных только из идеализированных источников напряжения, связаны между собой однозначной зависимостью, которая определяется компонентным уравнением данной ветви. Таким образом, зная токи всех ветвей электрической цепи, можно определить напряжения этих ветвей.

Пусть линейная электрическая цепь состоит только из идеализированных двухполюсных пассивных элементов: сопротивлений, емкостей, индуктивностей, а также неуправляемых источников напряжения. Основная система уравнений электрического равновесия такой цепи будет содержать q - 1 уравнений баланса токов, р - q + I уравнений баланса напряжений и р - р„„ компонентных уравнений для определения р неизвестных токов и р - /?ин неизвестных напряжений ветвей (напряжения рин ветвей, состоящих только из источников напряжения, заданы). Если каким-либо образом определить токи всех ветвей, то неизвестные напряжения могут быть найдены с помощью р - Раи компонентных уравнений. Для определения р неизвестных токов ветвей можно воспользоваться q - 1 уравнениями баланса токов Ир - q -\- I уравнениями баланса напряжений, выразив в последних напряжения ветвей через соответствующие токи. Таким образом, для цепи, не содержащей источников тока, применение метода тока ветвей позволяет уменьшить число уравнений, входящих в систему уравнений электрического равновесия от 2р - Рин до р.

Пример 4.1. Составим систему уравнений электрического равновесия по методу токов ветвей для электрической цепи, схема которой приведена на рис. 4.1, а. Граф этой цепи, соответствующий сокращенному топологическому описанию, изображен на рис. 4.1, б. Как видно из рисунка, для данного топологического описания число ветвей р = 6, число узлов q = 4, причем ни одна из ветвей не содержит источников тока (р„т - О) и не составлена только из источников напряжения (рин = 0). Выбирая дерево графа и систему независимых контуров в соответствии с рис. 4.1, в - д, составим основную систему уравнений электрического равновесия, которая будет включать в себя 12 уравнений, в том числе q - 1 =5 уравнений баланса токов:

-/i + 4 + /4 = 0;

-/4-44-/6 = 0; (4.1)

-/2-/з + /5 = 0,

р + t = 3 уравнения баланса напряжений:

t/, + (>6+t/e = 0; (4.2)

f)l-f>2 + f>3 = 0

II р = 6 компонентных уравнений

Ui = Z Jy~Ei: U, = Z J\-

V = Zj,-E- Vb = Zh\ (4.3)

U., = Z is; OsZU-

Подставляя уравнения (4.3) в (4.2), получим в сочетании с уравнениями (4.1) сокращенную систему уравнений электрического равновесия рассматриваемой цепи

- Л + Л, + /4 = 0: 2i /;+£4 /,+Ze /в = £i; -/4-/5i /в = 0; Zj., + Zj, h + Z tI»E; -i-ts+ibO; Zl ii~-Zl., + Zj.= E,-E„.

(4.4)

Таким образом, число одновременно решаемых уравнений уменьшилось от 12 до 6.

Рассмотрим более общий случай, когда исследуемая цепь помимо указанных ранее элементов включает в себя р„т ветвей, содержащих неуправляемые источники тока (ток этих ветвей задан, а напря-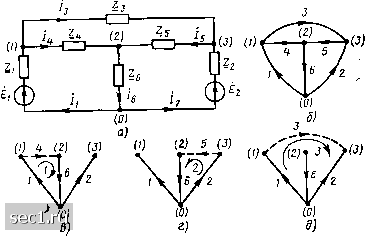

Рис. 4.1. К примеру 4.1

жение неизвестно). Выберем дерево графа цепи таким образом, чтобы ветви, содержащие источники тока, не входили бы в число ветвей дерева, т. е. являлись бы главными ветвями. Тогда напряжения этих ветвей будут фигурировать только в уравнениях баланса напряжений, составленных для главных контуров, замыкаемых ветвями, со-

держащими источники тока. Выражая в остальных р - р„г - Я 4-1 уравнениях, составленных на основании второго закона Кирхгофа, напряжения ветвей через токи этих же ветвей, получим в сочетании с q - \ уравнениями, составленными на основании первого закона Кирхгофа, р - уравнений для определения р - неизвестных токов ветвей.

Пример 4.2. Используя метод токов ветвей, составим систему уравнений электрического равновесия цепи, эквивалентная схема которой для мгновенных значетт приведена на рис. 1.39, а комплексная схема замещения - на рис. 4.2, а.

Как было показано в примере 1.7, основная система уравнений электрического равновесия этой цепи включает в себя 4 компонентных уравнения и 6 уравнений, составленных на основании законов Кирхгофа. Если дерево графа выбрано таким образом, что ветвь, содержащая источник тока, вошла в число главных ветвей (рис. 4.2, б), то напряжение этой ветви будет фигурировать только в одном уравнении, составленном на основании второго закона Кирхгофа.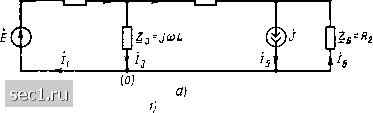

(/) 2 (2) (3)

г) и- (J) (1) (2) (3)

Рис 4 2. к примеру 4 2

Это уравнение, после нахождения пюков всех ветвей, можно использовать для определения неизвестного напряжения на источнике тока. Выражая в оставшихся уравнениях напряжения всех ветвей через соответствующие токи, постучим систему уравнений для определения пяти неизвестных токов ветвей:

•/, = 0;

Далее будет показано, что число ветвей цепи, токи которых могут быть заданы независимо, не может превышать числа главных контуров цепи р - q + 1. Когда рит = р - q + 1, число неизвестных токов ветвей будет равно q - I и они могут быть определены из q - I уравнения баланса токов.