Из полученных выражений видно, чпю комплексный коэффициент передачи рассматриваемой цепи по току от зажимов 5-5 к зажимам Б-6 и комплексная передаточная проводимость этой цепи от зажимов 1-Г к зажимам 6-6 (номера зажимов совпадают с номерами ветвей) равны соответственно:

(/ш) = [222з i-Z, (ZZ.)\,[ZM.(l2+l3) (Zi+Ze)!; Y,, (/w)= -2з/22 2з+(2, + 2з) (fi + Ze)!-

Метод наложения оказывается весьма эффективным и при анализе линейных цепей, находящихся под воздействием колебаний сложной формы. В этом случае сложное внешнее воздействие представляют в

лг)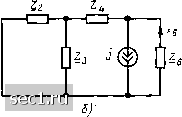

Рис. 4.9. К примеру 4.8

виде конечной или бесконечной суммы колебаний более простой формы, реакция цепи на воздействие которых может быть определена с помощью известных методов (подробнее см. гл. 6).

Необходимо отметить, что принцип наложения применим только для определения токов или напряжений линейной электрической цепи и не может быть использован для нахождения величин, которые не являются линейными функциями токов или напряжений. В частности, мощность, потребляемая каким-либо участком линейной электрической цепи, находящейся под воздействием нескольких независимых источников, не равна сумме мощностей, потребляемых этим же участком при воздействии каждого из независимых источников в отдельности.

Теорема взаимности

При изучении методов формирования уравнений электрического равновесия было установлено, что матрицы контурных сопротивлений и узловых проводимостей линейных цепей, составленных только из сопротивлений, емкостей, индуктивностей и независимых источников тока или напряжения, являются симметричными относительно главной диагонали. Можно показать, что симметричность этих матриц не нарушится и в том случае, когда в цепи имеется произвольное количество связанных индуктивностей. На симметричности матриц узловых проводимостей и контурных сопротивлений основано важное свойство линейных пассивных электрических цепей, которое формулируется в виде теоремы взаимности, или обратимости.

Рассмотрим линейную пассивную электрическую цепь, составленную из сопротивлений, емкостей и индуктивностей (в том числе и связанных).

В соответствии с теоремой взаимности контурный ток k-ro контура цепи, вызванный действием единственного независимого источиака напряжения, помещенного в i-й контур, равен контурному току (-го контура, вызванному действием того же источника напряжения, перенесенного из /-го контура в k-й.

Для доказательства теоремы выделим из рассматриваемой цепи главные ветви k-ro и i-ro контуров, а остальную часть цепи изобразим в виде четырехполюсника. Если независимый источник напряжения

Рис. 4.10. К доказательству теоремы взаимности (внешнее воздействие задано и виде источника напряжения)

Ё помещен в г-й контур (рис. 4.10, а), то в соответствии с выражением (4.14) контурный ток k-ro контура

(4.28)

Аналогичным образом находим контурный ток г-го контура, вызванный действием того же источника напряжения £, перенесенного из (-Г0 контура в/г-й (рис. 4.10,6):

4=А,,£,,/Д=Д,; Ё.

(4.29)

Выражения (4.28) и (4.29) отличаются только порядком индексов в алгебраических дополнениях А и А,-. Учитывая симметричность матрицы контурных сопротивлений рассматриваемой цепи относительно главной диагонали, нетрудно прийти к выводу, что Д = Д, а следовательно, Д =

Теорема взаимности для случая, когда внешнее воздействие на цепь задается в виде независимого источника тока, может быть сформулирована следующим образом.

Если независимый источник тока J, подключенный к какой-либо паре зажимов линейной пассивной цепи, вызывает на другой паре зажимов напряжение и (рис. 4.11, о), то этот же источник тока, подключенный ко второй паре зажимов (рис. 4.11, 6), вызовет на первой паре зажимов то же напряжение U.

Доказательство этой теоремы взаимности производится гак же, как это было сделано при питании цепи от независимого источника напряжения.

Если электрическая цепь удовлетворяет теореме взаимности (в любой формулировке), то говорят, что она обладает взаимностью (обратимостью). Электрические цепи, обладающие

взаимностью, называются взаимными (обратимыми). Если электрическая цепь не обладает взаимностью, то она является н е-взаимной (необратимой). К необратимым цепям относятся, в частности, нелинейные цепи (элементы матриц контурных сопротивлений и узловых проводимостей таких цепей зависят от токов или напряжений ветвей) и цепи, содержащие зависимые источники (матрицы контурных сопротивлений и узловых проводимостей таких цепей, как правило, несимметричны относительно главных диагоналей).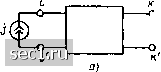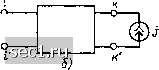

Рис. 4.11. К доказательству теоремы взаимности (внешнее воздействие задано в виде источника тока)

Применение теоремы взаимности в сочетании с принципом наложения позволяет в ряде случаев существенно упростить определение тока или напряжения какой-либо ветви электрической цепи, содержащей несколько независимых источников напряжения или тока.

Пример 4.9. Пусть, например, линейная электрическая цепь содержит N независимых источников напряжения £3, Ei.....Ё, размещенных соответственно в ветвях], 2, i, N. Определим ток k-й ветви, не содержащей источников энергии. Найдем сначала токи /**, 7*, .., соответственно 1, 2, .... (, N ветвей цепи, вызванные действием некоторого дополнительного источника э.д.с. Ell, помещенного в k-ю ветвь, при выключенных источниках £2..... Ej, £д,. Далее, в соответствии с теоремой взаимности найдем частичные токи вызываемые в k-й ветви действием каждого из источников Ёi в отдельности. Если бы э.д.с. источника, расположенного в i-й ветви, Ei, была равна Ejf, то согласно теореме взаимности частичный ток k-й ветви, /Jj*, вызванный действие.ч источника, расположенного в i-u ветви, был бы равен /**. Если El Ф Efi, то частичный ток k-й ветви /* вызванный действием э.д.с. Ei, пропорционален /{•**:

Суммируя частичные токи, вызванные действием всех независимых источников напряжения, находим

i= 1

Таким образом, анализ сложной электрической цепи, содержащей N независимых источников напряжения, свелся к определению токов N ветвей более простой цепи, содержащей один независимый источник напряжения.