Теорема компенсации

Теорема компенсации формулируется следующим образом: токи и напряжения произвольной электрической цепи не изменятся, если любую ветвь этой цепи заменить либо идеальным источником напряжения, э.д.с. которого равна напряжению данной ветви и направлена противоположно этому напряжению, либо идеальным источником тока, ток которого равен току рассматриваемой ветви и совпадает с ним по направлению.

Теорема компенсации базируется на общих свойствах основной системы уравнений электрического равновесия цепи и не накладывает ограничений на тип рассматриваемой цепи или характер внешнего воздействия. Рассмотрим, например, линейную электрическую цепь, находящуюся под гармоническим воздействием. Выделим в данной

к 1,

г.) II

Рнс. 4.12. К доказательству теоремы компенсации

цепи произвольную ветвь, комплексное сопротивление которой равно Z,j (рис. 4.12, а). Напряжение и ток этой ветви связаны уравнением,

составленным на основании закона Ома в комплексной форме = = Zft/. В соответствии с теоремой компенсации выделенную ветвь можно заменить либо идеальным источником напряжения, э. д. с; которого равна напряжению данной ветви Ё = 0 Z,if, и направлена навстречу этому напряжению (рис. 4.12, б), либо идеальным источником тока, ток которого равен току рассматриваемой ветви j = = Д = UfJZ,, и совпадает с ним по направлению (рис. 4.12, в). Составляя основную систему уравнений электрического равновесия каждой из цепей (рис. 4.12, б, в), убедимся, что она совпадает с основной системой уравнений электрического равновесия исходной цепи. Действительно, при формировании уравнений электрического равновесия исходной цепи напряжение f/ = ZjJ на выделенной ветви учитывается со знаком плюс в левой части уравнений баланса напряжений, составленных для контуров, содержащих рассматриваемую ветвь (предполагается, что направление обхода этих контуров совпа-. дает с направлением тока 1). При составлении уравнений электрического равновесия цепи (рис. 4.12, б) член Uf = Z/ в левой части соответствующих уравнений отсутствует, однако в правой части этих уравнений появляется член -£ = -U,, = -Zj. Следовательно, замена комплексного сопротивления Z идеальным источником напряжения Ё - Zjk соответствует переносу члена Zjf из левой час-

ти уравнений баланса напряжений в правую с соответствующим изменением знака.

При составлении уравнений электрического равновесия исходной цепи (рис. 4,12, а) ток выделенной ветви учитывается в левой части уравнений баланса токов; соответствующие уравнения преобразованной цепи (рис. 4.12, в) вместо тока протекающего через комплексное сопротивление Z, содержат равный ему ток У = 4 = ft/ идеального источника тока. Таким образом, цепи, схемы которых приведены на рисунке, являются эквивалентными.

Необходимо отметить, что источники напряжения и тока, заменившие в соответствии с теоремой компенсации сопротивление ветви Z, зависимые: э. д. с. источника напряжения Ё прямо пропорциональна

току ветви, содержащей этот источник, а ток источника тока У прямо пропорционален напряжению источника тока. Из эквивалентности испей следует, что идеальный источник напряжения, э. д. с. которого пропорциональна отдаваемому току (Ё - Z/ft), и идеальный источник тока, ток которого прямо пропорционален напряжению на зажимах источника (У = UjZf), могут быть заменены комплексным сопротивлением

z, = £/4=(y,/y.

Теорема компенсации расширяет возможности эквивалентных преобразований электрических цепей.

Автономные и неавтономные двухполюсники

Рассмотрим произвольный линейный двухполюсник, содержащий наряду с идеализированными пассивными элементами управляемые и неуправляемые источники тока или напряжения. Представляют нн-тсрес два предельных режима работы такого двухполюсника: режим холостого хода, когда ток внешних выводов двухполюсника равен нулю, и режим короткого замыкания, при котором напряжение между внешними выводами двухполюсника равно ну..о. Напряжение между выводами двухполюсника в режиме холостого хода называется напряжением холостого хода,\ а ток между выводами двухполюсника в режиме короткого замыка- ния - током короткого замыкания.

Двухполюсник, напряжение холостого хода или ток короткого замыкания которого не равны нулю, назовем автономным. Очевидно, что автономный двухполюсник должен содержать один или несколько нескомпенсированных независимых источников, т. е. таких источников, сумма частичных реакций на воздействие которых на внешних зажимах двухполюсника не равна тождественно нулю.

Если напряжение холостого хода и ток короткого замыкания двухполюсника тождественно равны нулю, то такой двухполюсник будем называть неавтономным. Неавтономный двухполюсник не мо-

8 Зак 565 - 225

жет содержать нескомпенсированных независимых источников, т. е. в его состав могут входить только идеализированные пассивные элементы и управляемые источники тока или напряжения. Таким образом, активные двухполюсники могут быть автономными или неавтономными, а пассивные двухполюсники представляют собой частный случай неавтономных.

Комплексным входным сопротивлением Z неавтономного двухполюсника называется отношение комплексной амплитуды напряжения на его зажимах к комплексной амплитуде тока (заметим, что данное ранее определение комплексного входного сопротивления пассивного двухполюсника естественным образом вытекает из этого определения). Если неавтономный двухполюсник не содержит управляемых источников, т. е. является пассивным, то его комплексное входное сопротивление может быть найдено, например, путем постепенного сворачивания схемы двухполюсника с использованием методов преобразования пассивных цепей. В общем случае комплексное входное сопротивление неавтономного двухполюсника находят методом пробного источника, в соответствии с которым к входу исследуемого двухполюсника подключают произвольный независимый источник напряжения или тока (пробный источник) и определяют отношение комплексных действующих значений напряжения и тока на внешних зажимах двухполюсника.

Пример 4.10. Определим комплексное входное сопротивление неавтономного двухполюсника, схема которого изображена на рис. 4.13, а (задачи такого типа часто встречаются на практике, например при определении комплексного входного сопротивления усилительного каскада на полевом транзисторе).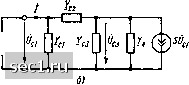

Рис 4 1Л К примеру 4.10

Подключим к входным зажи.на.ч исследуемой цепи пробный источник напряжения е =~ Ё (рис. 4.13, б) и найде.н комплексное действующее значение входного тока двухполюсника

1- jwC.E I /шС2(Я- Ucs).

Для определения комплексного действующего значения напряокения на емкости Сз состави.и уравнение электрического равновесия цепи (рис. 4.13, б) по методу узловых напряжений

откуда

Е.