Используя выражение (4.30), найдем значение э. д. с. Ei, при котором частичный ток а-й ветви Д" = 0:

ЁЁи. (4.31)

Таким образом, если э. д. с. вспомогательных источников выбрать равными напряжению холостого хода автономного двухполюсника (/х, то ток ветви /„ будет равен частичному току ti создаваемому действием источника напряжения Ё, при выключении независимых источников, входящих в состав автономного двухполюсника, и выключении источника напряжения fj.

Используя эквивалентную схему для определения частичного тока Д"", находим

L = > =х/(2„„ + ZJ = £з„/(4„ 4- ZJ, (4.32)

где Zpa - комплексное входное сопротивление исходного автономного двухполюсника, равное комплексному входному сопротивлению приведенного на рис. 4.16,6 неавтономного двухполюсника НД. Как видно из выражения (4.32), ток а-й ветви исходной цепи (см. рис. 4.15, а) равен току некоторой цепи, содержащей помимо сопротивления Z„ источник напряжения Ёж = и комплексное сопротивление ZaK = Z„o (см. рис. 4.15, б). Итак, ток выделенной ветви не изменился при замене автономного двухполюсника эквивалентным источником энергии, э. д. с. которого равна напряжению холостого хода автономного двухполюсника, а внутреннее сопротивление - его комплексному входному сопротивлению.

Переходя от последовательной схемы замещения эквивалентного

источника к параллельной, можно показать, что значение тока независимого источника тока (см. рис. 4.15, в) равно току короткого замыкания автономного двухполюсника, а внутренняя проводимость

Kg к - его комплексной входной проводимости Y = аа-

Воспользовавшись теоремой об эквивалентном источнике, можно найти последовательную или параллельную схемы замещения любого сколь угодно сложного линейного активного двухполюсника, поэтому данную теорему часто называют теоремой об активном двухполюснике. Эта теорема позволяет существенно упростить анализ цепей, особенно в тех случаях, когда требуется определить ток или напряжение только одной ветви сложной цепи, содержащей большое количество управляемых и неуправляемых источников тока и напряжения. В связи с тем что параметры элементов последовательной и параллельной схем замещения активного двухполюсника легко поддаются измерениям, выполняемым на внешних зажимах, теорему об эквивалентном источнике применяют и для построения эквивалентных схем активных двухполюсников по результатам их экспериментального исследования.

Пример 4.12. Используя теорему об эквивалентном источнике, определим ток /с цепи, комплексная схема замещения которой приведена на рис. 4.2, а.

Выделим из рассматриваемой цепи ветвь, содержащую сопротивление Zj, и представим остальную часть цепи, которую можно рассматривать как автономный двухполюсник, последовательной схемой замещения (рис. 4.17, а). Э.д.с.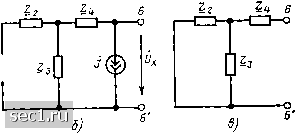

Рис. 4.17. К примеру 4.12

источника напряжения Яэк определяется как напряжение холостого хода на зажимах автономного двухполюсника, схема которого приведена на рис. 4.17, б:

£эк = х= {2з £-[Z, Z3 + Z, (£, + з)] y>/(Z, Z.,).

Внутреннее сопротивление эквивалентного источника равно входному сопротивлению неавтономного двухполюсника (рис. 4.17, в):

2эк- £4-h Z2Z3/(Z2-J-Z3).

Наконец, используя преобразованную схему рассматриваемой цепи (рис 4.17, а), находим искомый ток

-£эк 22£з+24 (Z + Za)]/- ZE

2б + .ZaK ~ Zaz-f-{Z + Z,) (Z4-гZ)

§ 4.3. МЕТОД СИГНАЛЬНЫХ ГРАФОВ

Общие представления о сигнальных графах

Решение уравнения электрического равновесия сложных цепей даже в численной форме весьма трудоемко. Задача анализа цепи становится особенно сложной тогда, когда неизвестные токи и напряжения или комплексные частотные характеристики должны быть найдены в виде аналитических соотношений. В ЭТИ.Х случаях весьма полезным может оказаться применение метода сигнальных графов, который позволяет упростить решение уравнений электрического равновесия линейных электрических цепей в аналитическом виде (символьной форме).

Как известно, сигнальный граф, или направленный граф прохождения сигналов, представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в .электрической цепи. Узлы (вершины) такого графа соответствуют входящим в эту систему неизвестным величинам (токам и напряжениям ветвей, контурным токам, узловым напряжениям) и величинам, характеризующим внешние воздействия на цепь (токам независимых источников тока, э. д. с. независимых источников напряжения, контурным э. д. с, узловым токам). Ветви сигнального графа отображают причинно-с.1едствеиные связи между величинами, соответствующими отдельным узлам. В рамках метода сигнальных графов эти величины называются с и г и а-

л ?. м и. Каждой ветви сигнальногв графа приписывается определенное направление и присваивается весовой коэффициент, который называется передачей ветви. Узлы сигнального графа обозначают теми же буквами, что и соответствующие узлам величины; направления ветвей показы-рают стрелками, около которых указывают передачу ветви.

Если ветвь с передачей А направлена от узла xi к узлу Xj (рис. 4.18, а),

Axi, (4.33)

следовательно, при прохождении через ветвь сигнал умножается на передачу ветви. Разрешим уравнение (4.33) относительно xf.

Xi - Xj/A. (4.34)

Сигнальный граф, соответствующий этому уравнению (рис. 4.18,6), будет отличаться от сигнального графа, соответствующего уравнению (4.33), направлением и передачей ветви. Таким образом, вид сигнального графа зависит от того.

-оХ:

-oXj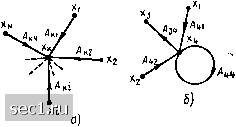

Рис. 4.18. Сигнальные графы, соответствующие выражениям (4.33) (а) и (4.34) (б)

Рис 4.19. Суммирование сигналов в узле сигнального графа

относительно какой из величин разрешено заданное уравнение, т. е. от того, какая из величин рассматривается как причина, а какая - как следствие.

Если в узле Xk сходится несколько ветвей (рис. 4.19, а), то значение сигнала в этом узле будет равно сумме сигналов всех входящих в него ветвей:

Xk--- AkiXf, (4.35)

где N - число ветвей, направленных к узлу Xk, Ai - передача ветви, направленной от узла Xi к узлу Xk- Ветви, направленные от узла Xk, на сигнал в этом узле не влияют и прн подсчете Xk не учитываются. В число ветвей, направленных к рассматриваемому узлу, могут входить и ветви, начинающиеся в данном узле (рис. 4.19, б). Такие ветви называются петлями. Значение переменной в узле, к которому подключена одна или несколько петель, находится по общему правилу (4.35), например (на рис. 4.19,6)

Xi --- AiiXi f Аг -I- 44 Xf (4.36)

Из выражения (4.36) видно, что при наличии петель, подключенных к какому-либо узлу, переменная, соответствующая этому узлу, входит и в левую, и в правую часть уравнения (4.35).

Рассмотрим некоторые понятия, относящиеся к сигнальным графам.

Истоком называется узел сигнального графа, от которого направлены все примыкающие к нему ветви. Узел сигнального графа, к которому направлены все примыкающие к нему ветви, называетси стоком. Узлы, которые имеют как входящие, гак н исходящие ветви, называются смешанными. Например, в графе (рис. 4.18, д) узел дс; - исток, у.зел дс - сток; в графе (рис. 4.19, б) узлы и -- истоки, узел Хз - сток, узел дс, - смешанный.