Если сигнал, соответствующий некоторому узлу сигнального графа, не выражается через сигналы других узлов, то такой узел является независ и-и ы м. Если сигнал, соответствующий какому-либо узлу, выражается через сигналы других узлов, то такой узел является зависимым. К независимым узлам относятся истоки, к зависимым-стоки и смешанные узлы Очевидно, что уравнения вида (4.35) могут быть составлены только для зависимых узлов.

• ••••

Пример 4.13. В сигнальном графе (рис. 4.20) узлы дсв, - истоки, узел JC5 - сток, узлы 2, лгз и относятся к смешанным. Для зависимых узлов х- хь можно составить систему уравнений

= 0*1 + ftjCj + схз + dxt;

Х2 = exi + fx2 + hxt;

хз = gxi;

«4 = kxg + тхз + nx;

Хь = PXf.

Путь между узлами xt и xj сигнального графа - это непрерывная последовательность однонаправленных ветвей, связывающая узел xi с узлом xj и проходящая через каждый узел графа не более одного раза. Произведение передач ветвей, образующих путь между узлами xi и xj, называется передачей пути Pji. Так, между узлами хл и Xi сигнального графа (рис. 4.20) можно указать три пути с передачами = dgkp (ветви d, g, k к р), Я* = = dgmp и Pg> = denp. Последовательность ветвей d. с, т ж р w образует пути от вершины Хй к вершине хь, так как направление ветви с не совпадает с направлением пути.

Замкнутый путь, который начинается н заканчивается в одном узле, называется контуром. Очевидно, что петля есть частный вид контура, в который входит одна ветвь. Произведение передач всех ветвей, входящих в /-й контур, называется передачей контура Lj. На рис. 4.20 можно выделить четыре г, л пп v ю

контура с передачами Lbe Рис. 4 20. К примеру 4.13

(ветви b и е), Lj = gr (ветви g

и с), Z.3 = а (петля а) и = f (петля f). Ветви ft и m не образуют контура, так как они не представляют собой замкнутой последовательности однонаправленных ветвей. Такие ветви называются параллельными.

Два контура или контур и путь называются соприкасающимися, если они имеют общие узлы. Если два контура или контур и путь не имеют общих узлов, то они являются несоприкасающимися. На рисунке контуры с передачами Lgc и Li~j;L3 = a и Li = f являются несоприкасающимися, а контуры с передачами - be и = gc; = be и l.i=f, = = be и Lg a - соприкасающимися. Контур с передачей L4 == / не соприкасается с путями PsV и f 5б*> "° соприкасается с путем Р). Как видно нз примера 4.13, каждому сигнальному графу .можно однозначным образом поставить в соответствие систему линейных алгебраических уравнений, составленных относительно сигналов зависимых узлов.

Для решения обратной задачи - построения сигнального графа, соответствующего заданной системе уравнений, эта система уравнений должна быть приведена к причинно-следственной форме, т. е. каждое из входящих в систему уравнений должно быть разрешено относительно одной из переменных (различных для каждого из уравнений). Далее, определяется общее число узлов графа Л, которое равно сумме числа неизвестных переменных и числа ненулевых сво-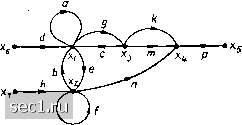

бодиых членов уравнений. Построение сигнального графа начинается с нанесения точек, соответствующих его узлам. Затем узлы графа, в соогветствии с системой уравнений, приведенной к причинно-следственной форме, соединяются между собой ветвями так, чтобы сумма сигналов всех ветвей, сходящихся в каждом узле, равнялась бы значению сигнала этого узла.

Хотя свойства сигнального графа не зависят от формы и длины ветвей, а также от взаимного расположения узлов графа на плоскости чертежа, с целью повышения наглядности рекомендуется истоки располагать в левой части чертежа, стоки - в правой, а остальные узлы - между ними.

В связи с тем что одну и ту же систему уравнений можно различными способами привести к причинно-следственной форме, каждой системе уравнений можно поставить в соответствие некоторое множество графов. Различные графы, соответствующие одной и той же исходной системе уравнений, называются равносильными. Рассмотрим несколько примеров построения графов, соответствующих заданной системе уравнений.

соответствующий системе

Пример 4.14. Построим сигнальный граф, уравнений

onxl + «12*2 + "13x3 = bi\

"21*1 + "22*2 + as3«3 = 2;

ОзЛ + а 32*2 + 083*3 = 0.

Приведем данную систему уравнений к причинно-следственной форме, для чего разрешим первое уравнение относительно х, второе - относительно х2, а третье - относительно х:

*1= -OuVaii - азХз/ац + Voii; *2 = - a2iV"2s - 023*3/022 + *2/а22; *з = - ОзЛ/азз - 032*2/033-Число независимых переменных в этой системе уравнений равно трем, число ненулевых свободных членов - двум, следовательно, общее число узлов сигнального графа равно пяти. Располагая в левой части чертежа независимые узлы, соответствующие свободным членам и Ь, а в правой части узлы, соответствую-

а] 61

Рис. 4.21. К примеру 4.14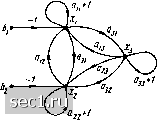

щие неизвестным величинам Хх, х, Хз, и соединяя их ветвями в соответствии с системой уравнений, преобразованной к причинно-следственной форме, получим сигнальный граф, изображенный на рис. 4.21, а.

Исходная система уравнений может быть приведена к причинно-следственной форме и другим способом. Прибавляя к правой и левой частям первого уравнения xl, второго х2, третьего х3 и выполняя преобразования, получим

xl =/(«11 + 1) *1 + «12*2 + «18*3 - Ь;

«2 =/«21*1 + («22 + 1) *2 + «2 3*3 - г". x, = 031*1 + «32*2 + ("зз + ) *3-

Этой системе уравнений соответствует сигнальный граф, изображенный на рис. 4.21, б.

Графы (рис. 4.21, а, б) имеют различную структуру и передачи ветвей, однако они соответствуют одной и той же исходной системе уравнений и поэтому являются равносильными. Очевидно, что если первое уравнение, входящие в исходную систему, разрешить не относительно х, а относительно х или Хз, то получатся другие варианты представления исходной системы уравнений в причинно-следственной форме, каждому из которых можно поставить в соответствие сигнальные графы, равносильные графам, изображенным на рис. 4.21.

Пример 4.15. Составим сигнальный граф, соответствующий узловым уравнениям цепи, схема которой приведена на рис. 4.2, а.

Узловые уравнения данной цепи были получены при рассмотрении примера 4.4.

Разрешая первое из уравнений относительно Озд, а второе - относительно U20, получаем

()s„ = Z4 (1 /£4 + 1 IZ,) U30+24 J:

г/зо = £4 (1/Z,+ I/Z3+I/Z4) t/jjo-Zf/Zj.

Этой системе уравнений соответствует сигнальный гра ф, приведенный на рис. 4.22.

Пример 4.16. Используя метод контурных токов, составим систему уравнений для определения тока Ig цепи, схема которой приведена на рис. 4.2, а. Построим такоше сигнальный граф, соответствующий этой системе уравнений.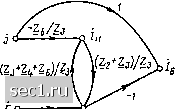

Рис. 4.22, К примеру 4.15 Рис. 4.23. К примеру 4.16

Контурные уравнения рассматриваемой цепи были сформированы при рассмотрении примера 4.3. Дополняя эти уравнения соотношением, связывающим ток /в с контурными токами и I22, получаем

(£,+£з) /„-2з4 = £;

-Z3 /ii + (Z3-bZ,+Z,) hi=-Zj:

/в-/+ 4 = 0.

Разрешим каокдое из этих уравнений относительно одной из неизвестных величин:

hi = (2а+2,) /и /2з -£(2з; /ii= (£s+24+2e) hjZ3-Z;j/Z3; hJ-hi.

Этой системе уравнений соответствует сигнальный граф, аэобважгнный на рис. 4.23. 1