Преобразования сигнальных графов

Используя правила построения сигнальных графов, соответствующих заданной системе уравнений, можно убедиться, что каждому равносильному преобразованию исходной системы уравнений соответствует некоторое преобразование сигнального графа и, наоборот, каждому преобразованию сигнального графа соответствует определенное преобразование исходной системы уравнений. На практике оказывается, что преобразования сигнальных графов выполняются проще и в более наглядной форме, чем преобразование соответствующих им уравнений. Поэтому при анализе цепей во многих случаях преобразование уравнений электрического равновесия заменяется преобразованием соответствующих сигнальных графов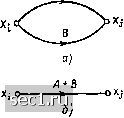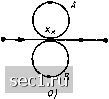

Рис. 4.24. Объедине- Рис. 4.25. Объедииеиие петель

ние параллельных ветвей

Рассмотрим основные преобразования сигнальных графов.

Объединение параллельных ветвей. Две параллельные ветви с передачами А я В могут быть заменены одной ветвью с передачей А -\- В. Действительно в соответствии с рис. 4.24, а сигнал в узле, к которому сходятся ветви с передачами А к В, исходящие из узла xi, будет равен

Xj=Axi-\-Bxi, или Xj=(A-\-B) XI.

Последнему уравнению соответствует сигнальный граф, имеющий одну ветвь с передачей А -\- В, направленную от узла xi к узлу xj (рис. 4.24, б). Правило объединения параллельных ветвей обобщается на любое число параллельно включенных ветвей, его можно применять для объединения петель, подключенных к одному узлу (рис. 4.25).

Объединение последовательности однонаправленных ветвей. Две последовательно включенные однонаправленные ветви с передачами А » В могут быть заменены одной ветвью с передачей АВ.

Действительно, графу, приведенному на рис. 4.26, а может быть поставлена в соответствие система уравнений

Xj = Axi;

Xk = Bxj. (4.37)

Исключая из (4.37) переменную xj, получаем

Xk = ABxi. (4.38)

Уравнению (4.38) соответствует сигнальный граф, содержащий одну ветвь с передачей А В (рис. 4.26, б). Рассмотренное преобразование представлиет собой частный случай устранения смешанного узла сигнального графа.

Устранение промежуточного узла. Смешанный узел, к которому подключено несколько не образующих контуров ветвей, причем только одна из ветвей направлена к узлу (рис. 4.27, д) или только одна из ветвей направлена от узла f (рис. 4.27, в), называется промежуточным.

Для устранения промежуточного узла первого типа, в которой входит только одна ветвь, составим систему уравнений

Хз = Вх; xs = Dx2 и исключим из нее переменную х:

Хз = АВх-;

«4 = ACxi, (4.39)

Хь = ADxj.

Системе уравнений (4.39) соответствует граф, не содержащий промежуточного узла Х2 (рис. 4.27, б). Аналогичным образом устраняется промежуточный узел, в который входит несколько ветвей, а выходит только одна (рис. 4.27, г).

> о

а) АВ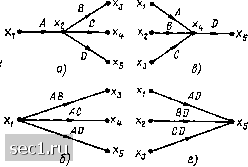

Рис. 4.26. Объединение последовательности однонаправленных ветвей

Рис. 4.27. Устранение промежуточного узла, из которого исходит (д, б) и в который входит (в, г) несколько ветвей

Устранение контура. Сигнальному графу, изображенному на рис. 4.28, а, может быть поставлена в соответствие система уравнений

Х2 = Ах + СХз\

Хз ~ Вх.

Подставляя первое из этих уравнений во второе, получаем

Хз = ABxi + ВСхз. (4.40)

Уравнению (4.40) соответствует преобразованный граф, приведенный на рис. 4.28, б.

Исключение петли. Исключение петли с передачей А, подключенной к какому-либо узлу сигнального графа, сопровождается умножением передач ветвей, входящих в этот узел, на 1/(1 - А).

Действительно, для сигнального графа, приведенного на рнс. 4.29, а, можно составить систему уравнений

дсз = Axi + Вх2 + Сдсз;

Приводя в первом из этих уравнений подобные члены н разрешая его относительно Хз, получаем

Хз = Л V(l - С) + BxJ{\ - С);

х4 = Вхз. (4.41)

АВ/О-ВС)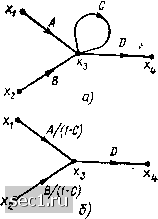

Рис. 4.28. Устранение контура

Рис. 4.29. Устранение петли

Как видно из соответствующего системе уравнений (4.41) сигнального графа (рис. 4.29, б), после устранения петли передачи ветвей, входящих в узел Xj, оказались умноженными иа 1/(1 - С), а передача ветви, выходящей из узла дГз, осталась без изменения.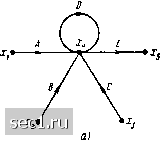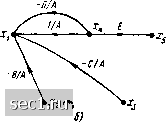

Рис. 4.30. Инверсия ветви

Применяя операцию устранения петли, преобразованный граф (см. рис. 4.28, б) можно заменить одной ветвью (см. рис. 4.28, в).

Инверсия (изменение направления) ветви. Рассмотрим некоторый граф (рис. 4.30, а), которому соответствует система уравнений

Xi = Axi + 8x2 + 0x3 + Dx; хь = Exi-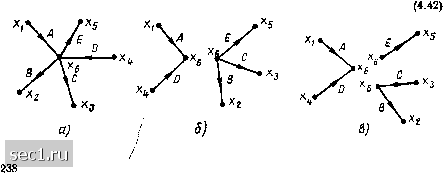

Рис. 4.31. Расщепление узла