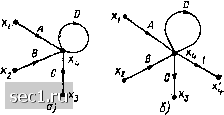Рис. 4.32. Удлинение узла

Пусть необходимо изменить направление какой-либо ветви, например, направленной из вершины х в вершину x. С этой целью разрешим первое из уравнений (4.42) относительно х:

Xl xJA - BxJA-CxlA-DxJA;

хв -~- Exi. (4.43)

Системе уравнений (4.43) соответствует сигнальный граф, изображенный на рис. 4.30, б. Как видно из сравнения рис. 4.30, а и б, инвертирование ветви, направленной от узла xi к узлу Xj, сопровождается изменением передач и точек подключения всех ветвей, ранее направленных к узлудс. Ветвь с передачей А, направленная от узла xi к узлу Xj, заменяется ветвью, направленной от узла Xj к узлу ж,, с передачей \1 А. Все ветви, ранее направленные к узлу Xj, заменяются ветвями, направленными к узлу xi, передачи этих ветвей умножаются на -МА, Ветви, не направленные ранее к узлу Xj, при Инвертировании ветви, направленной к Xj, остаются без изменений.

Расщепление узла. В связи с тем что сигнал в каждом узле сигнального графа определяется только сигналами входящих в него ветвей, .1юбой узел сигнального графа может быть расщеплен на два узла: один - содержащий все ветви, направленные к узлу, другой - направленные от узла. Так, узел Xi графа, изображенного на рис. 4.31, о, может быть расщеплен на два узла (рис, 4.31, б). Узел, который содержит только исходящие иа него ветви (исток), может быть расщеплен на произвольное количество узлов, не превышающее числа исходящих из него ветвей (рис. 4.31, я).

Удлинение узла. В ряде случае возникает необходимость в6 введении в сигнальный граф дополнительного узла, сигнал в котором совпадает с сигналом в одном из узлов Xj сигнального графа. Такая операция называется удлинением узла xj. Для удлинения узла xj этот узел должен быть соединен с вновь вводимым узлом xl ветвью, передача которой равна единице, Например,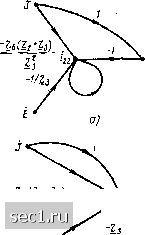

е) 3)

Рис. 4.33. к примеру 4.17

для удлинения узла (рис. 4.32, а) введем новый узел xi и соединим его с узлом Xt ветвью, передача которой равна единице (рис. 4.32, б).

Совместное проведение описанных преобразований позволяет, как правило, существенно упростить структуру сигнального графа. Конечной целью преобразований обычно является получение наиболее простого графа, не допускающего дальнейших упрощений. Такой граф называется конечным. Конечный граф не содержит смешанных узлов, а включает в себя только стоки и истоки.

Пример 4.17. Упростим сигнальный граф, изображенный на рис. 4.23. Для этого последовательно исключим контур (рис. 4.33, а), петлю (рис. 4.33, б), промежуточный узел (рис. 4.33, в) и объединим параллельные ветви (рис. 4.33,г). Преобразованный граф, (рис. 4.33, г) не содержит смешанных узлов и не подлежит дальнейше.му упрощению. Этот граф является конечным.

Применение сигнальных графов к анализу цепей

Применение метода сигнальных графов при анализе цепей оказывается весьма эффективным в тех случаях, когда требуется определить ток или напряжение только одной из ветвей цепи, а также найти ее комплексные частотные характеристики.

Как отмечалось, используя различные преобразования, исходный сигнальный граф можно привести к конечному. Если истоками графа являются узлы, сигналы которых Х; есть комплексные изображения величин, характеризующих внешние воздействия на зажимах i-i, а стоками - узлы, сигналы которых Yj представляют собой комплексные изображения искомых токов или напряжений ветвей, подключенных к зажимам /-/, то, используя конечный граф, можно записать соотношения, в явной форме выражающие зависимость искомых неизвестных токов и напряжений от величин, характеризующих внешние воздействия. Передача ветви Aji конечного графа, связывающей исток Xj со

стоком Yj, будет равна комплексной частотной характеристике цепи Нл (/со), измеренной в режиме, когда все источники внешнего воздействия, за исключением Xi, выключены.

Трудоемкость преобразования сигнального графа к конечному во многом определяется выбором исходной системы уравнений электрического равновесия и тем, каким образом осуществлен переход от исходной системы уравнений к сигнальному графу. Для уменьшения числа узлов сигнального графа в каче-<лъе исходной системы уравнений рекомендуется применять систему уравнений электрического равновесия цепи, составленную по методу узловых напряжений или контурных токов, дополнив ее уравнениями, связывающими искомые токи и напряжения с контурными токами или узловыми напряжениями.

Пример 4.18. Определим ток /в цепи, комплексная схема зажщения которой приведена на рис. 4.2, а, преобразуя сигна-тьный граф этой цепи (см. рис. 4.23) в конечный.

Граф, приведенный на рис. 4.23, соответствует контурным уравнениям рассматриваемой цепи, дополненным уравнением, выражающим связь искомого тока с контурными токами /ц, /.з " f зз- J (с.**, пример 4.16). Преобразование этого графа в конечный было проведено в примере 4. П. Непосредственно по виду конечного графа записываем выраоюение для искомого тока

/б = {[Z21з + Ь (£2 + 2з) I У -£з £} /{7.2 7.3 + (Z + £3) (£4+£«)].

которое совпадает с выражениями для этого тока, полученными с использованием метода наложения (см. пример 4.8) и теоремы об эквивалентном источнике (см. пример 4.12).

Передача ветви, связывающей исток J и сток Ig, равна комплексному коэффициенту передачи цепи по току Ges (jm) от зажимов 5-5 к зажимам 6-6 {номера зажимов совпадают с номерами ветвей) в режиме, когда источник Ё закорочен:

Об5 (/») =

£=0

ZsZ3 + (Zs + Z3) (Z,+Z,)

Передача ветви, направленной от истока Е к стоку h, равна передаточной проводимости цепи Yei (jut) в режиме, когда ветвь с источником тока J разомкнута:

у=о Z2Z3+(Z2 + Z3) (Z+Ze)

Следует отметить, что сведение исходного сигнального графа к конечному, особенно для сложных цепей, может оказаться трудоемким. Кроме того, если необходимо определить несколько неизвестных величии, эту процедуру приходится выполнять несколько раз. Поэтому в таких случаях для нахождения комплексных частотных характеристик цепи и неизвестных токов и напряжений целесообразно воспользоваться формулой Мейсона, которая позволяет вычислять передачи ветвей конечного графа Aji Hjt (/со) непосредственно по исходному сигнальному графу, не прибегая" к его преобразованиям.

Формула Мейсона имеет вид

Aji = И л (/со) = 2 Да) I А. (4.44)

где Д - определитель сигнального графа, численно равный определителю исходной системы уравнений; Pj-** - передача k-ro пути от истока Xj к стоку

Yj; Aft - алгебраическое дополнение й-го пути. Суммирование производится по всем возможным путям нз узла Xj в узел Yj. Определитель сигнального графа

&=l-Li + LiLj- 2 ii. Lj, im+..., (4.45)

i a i.l.m

где 2Z.j-сумма передач всех контуров сигнального графа; 2 LjL - сумма

произведений передач всех возможных пар несоприкасающихся контуров; 2 LjLjL-сумма произведений передач всех несоприкасающихся троек кон-i,/,m

туров и т. д. Алгебраическое дополнение k-ro пути также вычисляется по формуле (4.45), но при этом учитываются только контуры, не касающиеся пути Р*/.

Пример 4.19. Используя формулу Мейсона, определим передаточную проводимость Кб] С/ы) цепи, схема которой приведена на рис. 4.2, а).

Сигнальный граф, составленный с использованием контурных уравнений цепи, был приведен на рис. 4.23 (см. пример 4.16). Этот граф содержит единственный контур, передача которого

LiZ+yt (Z 3+Z,+ZJI{Z%).

Используя выражение (4.45), найдем определитель сигнального графа (J2 + gj») (£з-Ь24+2а) g2Z3 + (Za+Z3) (Z,+ Z.)

£з Zl