Вид ВАХ нелинейного управляемого 1У • \л \л резистивного элеменпш существен-R(u) Jl(t) ным образом зависит от схемы

включения элемента, т. е. от того, какой из электродов является общим S) S) г) для основного и управляющего кон-

туров.

Рис. 5.5. Условные графические обоз- На принципиальных электриче-начения нелинейных сопротивлений: ских схемах реальные нелинейные i-odplfo/TpKTepScTKSfife-J uL- резистивные элементы изображают

тонной .характеристикой: г - неэлектриче- С ПОМОЩЬЮ усТаНОВЛСННЫХ СТан-

ски управляемое дзртами ЕСКД УСЛОВНЫХ графиче-

ских обозначений. При построении эквивалентных схем цепей нелинейные резистивные элементы либо изображают в виде двухполюсников или многоплюсников (см. рис. 5.2), либо представляют схемами замещения, содержащими наряду с другими элементами идеализированные нелинейные сопротивления (рис. 5.5). Для неэлектрически управляемых сопротивлений рядом с «полочкой» на условном графическом обозначении сопротивления указывают буквенное обозначение соответствующей управляющей величины (рис. 5.5, г).

Уравнения электрического равновесия нелинейных резистивных цепей

Как и в случае линейных электрических цепей, задача анализа нелинейной резистивной цепи заключается в общем случае в определении токов и напряжений всех или части ветвей при заданных параметрах независимых источников энергии. Если нелинейная цепь включает в себя р ветвей, из которых pi„ ветвей содержат независимые источники тока, а состоят только из независимых источников напряжения, то для определения 2р - рит - Pmi неизвестных токов и напряжений можно воспользоваться р уравнениями, составленными на основании законов Кирхгофа, к р - рт- р„а уравнениями ветвей.

В связи с тем что токи ветвей дерева любой электрической цепи однозначно выражаются через токи главных ветвей, а напряжения главных ветвей - через напряжения ветвей дерева, при выборе дерева графа нелинейной резистивной электрической цепи в качестве ветвей дерева необходимо использовать ветви цепи, содержащие нелинейные элементы с S-образной характеристикой, и ветви с независимыми источниками напряжения, а в качестве главных ветвей следует выбирать ветви с источниками тока и ветви, содержащие нелинейные резистивные элементы с N-образной характеристикой. Нелинейные резистивные элементы с монотонной ВАХ могут входить как в состав ветвей дерева, так и в состав главных ветвей. Очевидно, что все уравнения основной системы уравнений электрического равновесия нелинейной резистивной цепи будут алгебраическими, причем, по крайнем мере, одно из компонентных уравнений будет нелинейным.

Аналитически разрешить такие уравнения можно только в исклю-тительных случаях, при некоторых специально подобранных видах [слинейности. Как правило, эти уравнения решают приближенными •исленными, графическими или графо-аналитическими методами. В ря-\е случаев исследование процессов в простейших нелинейных ре-•истивных цепях удается провести без составления уравнений элект-jH4ecKoro равновесия - путем выполнения различных преобразовали исходной цепи.

§ 5.2. ГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА НЕЛИНЕЙНЫХ РЕЗИСТИВНЫХ ЦЕПЕЙ

Простейшие преобразования нелинейных резистивных цепей

Рассмотрим простейшие эквивалентные преобразования, которые можно применять как при анализе нелинейных резистивных цепей постоянного тока, так и при анализе нелинейных цепей, находящихся под произвольным внешним воздействием.

Пусть участок цепи (рис. 5.6, а) содержит два последовательно включенных нелинейных сопротивления и R, вольт-амперные характеристики которых представлены на рис. 5.6, б. Очевидно, что при любом значении тока 1вх = = г\ = «2 напряжение - "f «вх на зажимах данного участка цепи равно сумме напряжений на каждом из нелинейных сопротивлений: «ВХ = - «1 (ii) + «2 (fa)-

Суммируя ординаты -: шисимостей «i (ti) и I. (ta), получаем зависи-яхть между напряже-ием Цвх и током вх на 4.1жимах рассматривае-1ЭГ0 участка цепи

(рис. 5.6, б). Таким образом, участок цепи, содержащий два последо-в5(тельно включенных нелинейных сопротивления, может быть заменен Э{ним нелинейным сопротивлением, ВАХ Ывх (гвх) которого получается гутем суммирования ординат ВАХ «i(Ji) и «2(is)сопротивлений. Ана-тэгичным образом можно заменить участок цепи, содержащий после-ii «вательно включенные линейное и нелинейное сопротивления, а так-«е участок цепи, представляющий собой последовательное соедине-л le произвольного количества линейных и нелинейных сопротивлений.

• ••••

Пример 5.1. Найдем, зависимость между током и напряжением участка Ч-пи (рис. 5 7, а), представляющего собой последовательное соединение линей-Ulo /?2 и нелинейного Ri сопротивлений, ВАХ и (i) и и (ii) которых приведены на рис. 5.7, б. Определим изменение напряжения Auj на линейном сопротив-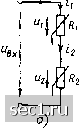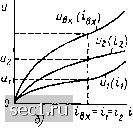

Рис. 5.6. Схема участка цепи с последовательно включенными нелинейными сопротивлениями (а) и их ВАХ (б)

лении /?2, соответсшующее приращению напряжения на зажимах цепи1их на

Вольт-амперную характеристику «вх (вх) рассматриваемого участка цепи получаем, суммируя ординаты ВАХ и (i) и и (i) последовательно включенных элементов. Используя эту характеристику (рис. 5.7, б), можно найти приращение тока цепи Дгвх, соответствующее изменению входного напряжения на Дивх- Далее, используя зависимость и (i-i), определяем соответствующее

вк

Рнс. 5.7. К примеру 5.1

данному приращению тока приращение напряжения Л«2 «а линейном сопротивлении. Как видно из рис. 5.7, б, приращение напряжения на линейном сопротивлении оказалось значительно меньше вызвавшего его изменение входного напряже ния Двх-

Рассмотрим участок цепи (рис. 5.8, а), представляющий собой параллельное включение двух нелинейных сопротивлений и R2, ВАХ к («i) ч h ("2) которых приведены на рис. 5.8, б. Как следует из пер-.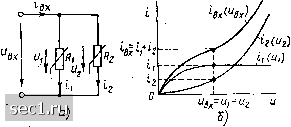

Рис. 5.8. Схема участка цепи с параллельно включенными нелинейными сопротивлениями (а) и их ВАХ (б)

вого закона Кирхгофа, входной ток Ibx рассматриваемого участка цепи при любом напряжении Ывх = «i = «г равен сумме токов нелинейных сопротивлений: tnx = h ("1) + «2 ("2)-

Суммируя ординаты зависимостей Д («]) и (uj), получаем ВАХ вх («вх) нелинейного сопротивления, которым можно заменить рассматриваемый участок цепи. Используя аналогичный прием, можно определить ВАХ участка цепи, содержащего произвольное количество параллельно включенных линейных и нелинейных сопротивлений.