емени. График х (t) расположим в нижней части рисунка так, чтобы X (О была параллельна оси х ВАХ, а ось времени - направлена ннз. Зависимость у-= у (t) построим в правой части рисунка так, чтобы ось времени была направлена вправо, а ось у (t) расположена параллельно оси у ВАХ.

Для определения реакции цепи на заданное внешнее воздействие необходимо для каждого момента времени t, выполнить следующие графические построения: по графику функции х (t) найти мгновенное значение внешнего воздействия х (t), затем по ВАХ определить соот-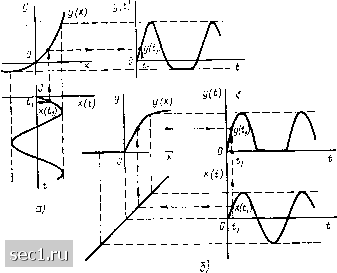

Рис. 5.18. Определение реакции безынерционного нелинейного резистивного элемента на заданное внешнее воздействие

петствующее этому внешнему воздействию мгновенное значение реак-,ии у (,) и построить точку с ординатой у (ti) на графике г/ -= г/ (t). Очевидно, что при увеличении количества точек на временной оси, для которых выполняются такие построения, точность определения реакции элемента на заданное внешнее воздействие возрастает.

Недостатком рассмотренного приема является то, что графики X (t) и у (t) построены в разных местах чертежа, а это неудобно при определении взаимно соответствующих точек на временных осях и затрудняет сравнение формы кривых х (t) и у (t).

Этот недостаток может быть устранен, если график х (t) построить непосредственно под графиком у (t) (рис. 5.18). В этом случае линии, проектирующие точки графика х = л: (i) на ВАХ у (х), перегнутся под углом 90 причем точки перегиба расположатся на некоторой вспомогательной прямой, проведенной под углом 45° к координатным осям через точку пересечения оси у ВАХ и оси времени зависимости х = = X (О-

зак 5ь5

x(t) I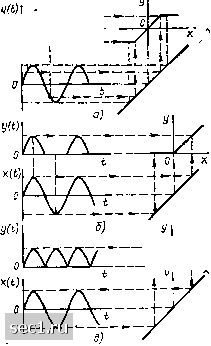

лебаний (рис. 5.19, периодное (рис. 5

Рис. 5.19. Определение вида ВАХ п., известной реакции безынерционного резистивного элемента на заданное внешнее воздействие

Как видно из рисунка, реакции нелинейной цепи иа гармоническое воздействие в общем случае не является гармонической функцией вре. мени.

Графические построения, приведенные на рис. 5.18, б, можно использовать и для решения обратной задачи - определения вида ВАХ безынерционного нелинейного резистивного элемента по известной

Жреакции этого элемента на заданное внешнее воздействие. . - Например, на рис. 5.19 показано, как, используя описанные графические построения, определить вид ВАХ нелинейных резистивных элементов, обеспечивающих двустороннее ограничение гармонических ко-а), однополупериодное (рис. 5.19, б) и двухполу-19, в) выпрямление переменного тока.

§ 5.3. АППРОКСИМАЦИЯ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ РЕЗИСТИВНЫХ ЭЛЕМЕНТОВ

Задача аппроксимации

Вольт-амперные характеристики реальных элементов электрических цепей обычно имеют сложный вид, их представляют в виде графиков или таблиц экспериментальных данных. В ряде случаев непосредственное применение ВАХ, задаваемых в такой форме, оказывается неудобным и их стремятся представить в виде достаточно простых аналитических соотношений, хотя бы качественно отражающих характер рассматриваемых зависимостей. Замена сложных функций приближенными аналитическими выражениями называется аппроксимацией (от лат. approximare - приближаться).

Аналитические выражения, аппроксимирующие ВАХ нелинейных резистивных элементов, с одной стороны (для повышения точности и достоверности анализа) должны как можно более точно описывать ход реальных характеристик, а с другой - повышение точности аппроксимации приводит, как правило, к усложнению аппроксимирующих выражений, что затрудняет как определение значений входящих в эти

выражения коэффициентов, так и применение этих выражений для анализа цепи. В связи с тем что характеристики однотипных нелинейных резистивных элементов от экземпляра к экземпляру отличаются за счет производственного разброса параметров и погрешности измерений, нецелесообразно стремиться получить аппроксимирующие выражения, точность которых превышает точность определения характеристик отдельных элементов. Таким образом, при решении задачи аппроксимации так же, как и при решении любой задачи, связанной с выбором расчетной модели, необходимо идти на компромисс между точностью и сложностью модели.

Успешное решение задачи аппроксимации в значительной степени зависит от ширины аппроксимируемой области ВАХ, т. е. от диапазона, в котором могут изменяться токи и напряжения исследуемого элемента. Как правило, чем уже область аппроксимации, тем более простой функцией может быть описана соответствующая ВАХ.

Задача аппроксимации ВАХ включает в себя две самостоятельные задачи: выбор аппроксимирующей функции и определение значений, входящих в эту функцию постоянных коэффициентов.

Выбор аппроксимирующей функции

Функцию, аппроксимирующую ВАХ какого-либо нелинейного резистивного элемента, выбирают либо исходя из физических представлений о работе данного элемента, либо чисто формально, основываясь на внешнем сходстве ВАХ с графическим изображением той или иной функции. Для аппроксимации ВАХ используют как элементарные, так и различные трансцендентные функции, а также степенные, экспоненциальные и тригонометрические полиномы и кусочно-линейные функции.

Так как внешнее сходство ВАХ с графическим изображением функции, выбранной в качестве аппроксимирующей, может оказаться обманчивым, перед тем, как перейти к определению значений коэффициентов соответствующей функции, желательно проверить возможность ее применения, используя метод выравнивания. Сущность этого метода заключается в том, что для проверки гипотезы о виде функциональной .•ависимости у - у {х), заданной множеством значений Xj, yj, переменные х vi у заменяют некоторыми новыми переменными X = f {х, у)\ Y - /2 (х, у), которые выбирают таки.м образом, чтобы при сделанных допущениях о виде функции у = у (х) переменные Y н X были связаны между собой линейной зависимостью

К - Л:,Х -f Ко- (5.4)

Таким образом, если проверяемая гипотеза о виде функции у ~= у (х) справедлива, то точки Xj - Д (Xj, yj), Yj = /2 {xj, yj) должны располагаться на одной прямой.

Если предполагается, что заданная зависимость описывается степенной функцией

у - ах", (5.5)