то, логарифмируя левую и правую части выражения (5.5) Ig у ~ ]g а + b \gx, нетрудно прийти к выводу о том, что зависимость между вспомогательными переменными Y -= \g у и X = \g х должна иметь линейный характер:

У = \ga + bX. (5.6)

Если зависимость между величинами у и х аппроксимируется показательной функцией

У -- ае", (5.7)

то линейной зависимостью

Y ]ga + {b\g е)Х (5.8)

будут связаны между собой переменные У -- \g у н X - - х. Для степенного полинома второй степени

у flo - ах + а,х (5.9)

линейный вид должна иметь зависимость Y Ау от X -= х, где \у -yj - yj-j - разность значений функции у (х), соответствующих двум соседним значениям аргумента Xj и Xj (предполагается, что значения аргумента образуют арифметическую прогрессию с шагом h).

Если заданная зависимость у - у (х) аппроксимируется экспоненциальным полиномом вида

у - as!" \- с, (5.10)

то линейной зависимостью

У - lga + (b\g&)X (5,11)

должны быть связаны вспомогательные функции У = \g {у - с) и X = X. Для определения с выбирают три значения аргумента Xi, Xi, Хд = (Ху -\г х12 и соответствующие им три значения функции у, у., и Уз, которые затем подставляют в выражение

с {УлУ2 - У1) (1/1 + .2 - 2г/з). (5.12)

Если при проверке гипотезы о виде аппроксимирующей функции методом выравнивания окажется, что зависимость между вспомогательными переменными X и У имеет линейный характер только в определенном диапазоне изменения X, то, следовательно, данная гипотеза справедлива только в соответствующем диапазоне изменения аргумента исследуемой функции у, (jCj).

Пример 5.5. На рис. 5.20, а изображена прямая ветвь ВАХ кремниевого диода. Проверим, можно ли аппроксимировать эту характеристику полиномом второй степени (5.9).

Выбираем шаг изменения аргумента h =~ 0.2 Ъ и рассчитываем значения вспомогательной переменной Y - у = yj - yj-i. соответспшующие выбранным значениям аргумента (рис. 5.20, б). Как видно из рисунка, зависимость Y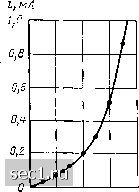

ОЛ 0,8 l,Z и,В а)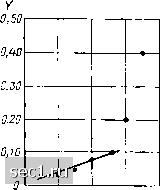

0,Ц- 0,8 1,2 X 5)

Рис. 5.20. К примеру 5.5

от X практически совпадает с линейной при изменении X ~ х в пределах от О до 1 В, следовательно, в этой области рассматриваемая В АХ может быть аппроксимирована полиномом второй степени.

Пример 5.6. Проверим, можно ли аппроксимировать ВАХ диода (см рис. 5 20, а) с помощью экспоненциального полинома вида (5.10).

Для определения константы с выберем три значения аргумента дг, О, л;. - 1, Хз~ 0,5 и найдем соответствующие им значения функции у1 - О, (/2 -" 0.3 и Уз 0,095, Подставляя эти значения в выражение (5.12). получаем с - -0,082. Далее строим зависимость вспомогательной функции Y -- Ig (у - - с) от X = X (рис. 5.21). Как видно из рисунка, в пределах от X О до X = 1 зависимость Y (X) практически совпадает с линейной, следовательно, в этой области рассматриваемая ВАХ может быть аппроксимирована экспоненциальным полиномом рассматриваемого типа.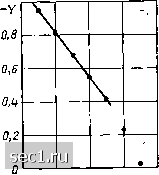

0,4- 0,8 t,2 X Рис, 5.21, К примеру 5,6

Из приведенных примеров следует, что задача выбора аппроксимирующей функции не имеет единственного решения. Выбор той или иной функции во

многом зависит от опыта и интуиции исследователя и в значительной степени определяется простотой нахождения значений коэффициентов функции и удобством ее применения для анализа.

Определение коэффициентов аппроксимирующей функции

Рассмотрим кратко основные методы определения коэффициентов аппроксимирующей функции. Наиболее часто для этой цели используют метод выбранных точек, в соответствии с которым зна-

чения коэффициентов аппроксимирующей функции определяют исходя из совпадения значений этой функции со значениями аппроксимируе. мой функции в ряде заранее выбранных точек, называемых узлами интерполяции (от лат. interpolare - подновлять). Если для аппроксимации ВАХ, задаваемой множеством точек {xj,yj], выбрана функция

у = y{x,ai,a2, ...,ап), (.5.13)

имеющая п неизвестных постоянных коэффициентов Oi, Oj, ,а„, то для определения этих коэффициентов выбирают п наиболее характерных точек ВАХ, лежащих в пределах рабочей области. Подставляя значения Xj и yj в каждой из выбранных точек в выражение (5.13), получают систему из п уравнений у = у (Xj, а,, a.i, a,j), решая которую, находят значения всех неизвестных коэффициентов. Очевидно, что такой выбор коэффициентов действительно обеспечивает совпадение значений аппроксимируемой и аппроксимирующей функций в узлах интерполяции, однако в промежутках между ними погрешность аппроксимации может быть весьма существенной (информация о ходе аппроксимирующей функции в них не учитывается), что является недостатком этого метода.

В отличие от метода выбранных точек метод наименьших квадратов обеспечивает наименьшую сумму квадратов отклонений I значений аппроксимирующей функции у -- (х, Oi, а., а„) от значений исходной функции у, (xj) в произвольном числе точек т, не связанном с числом неизвестных коэффициентов п:

/= I

Приравнивая нулю первые производные I по каждому из коэффи- циентов, получаем систему из п уравнений для определения п неизвестных числовых значений коэффициентов:

- = 2, 2 [у (X,., Ol, аг, ...,а„)-у]----0;

да а..

= у 2 [у (xj, «1, а,,..., a„)-yj]---=0.

оап дап

Метод наименьших квадратов требует весьма громоздких вычислений и применяется обычно только в тех случаях, когда необходима высокая точность аппроксимации.

Если гипотеза о характере аппроксимирующей функции проверялась методом выравнивания, то неизвестные значения коэффициентов аппроксимирующей функции могут быть определены по известным