2 O-i

Рис. 6.2. К примеру 6.2

Пример 6.2. Рассмотрим идеализированную цепь (рис. 6.2). Пусть в исходном состоянии ключ S находится в положении I, через индуктивность протекает постоянный ток (0 ), а ток индуктивности равен нулю-li,, (0 ) = E/R; (0 ) = 0.

Если в момент времени t = О ключ S перебросить из положения 1 в положение 2, то индуктивности Lj и окажутся включенными последовательно и их токи должны мгновенно уравняться (для соблюдения уравнения баланса токов). Очевидно, что такая коммутация некорректна, причем начальное значение тока индуктивностей (ii (0+) = ii2 С-ь) = L (+) после коммутации может быть определено из принципа непрерывности потокосцепления: Lll.l (0+) + Ц iL2 [Q+) = (h+L) X X (0+) = Liii (0 ), откуда

L(0+) = iii, (0 )/ (Li+L2)== = Li£/((L, 4-Lz)?l.

При анализе такой цепи обычно принимается, что токи индуктивностей Lj и Li скачком изменяются до уровня (Q+), а затем плавно увеличиваются, начиная с этого уровня, до установившегося значения ly, = E/R.

Можно убедиться, что энергия данной цепи непосредственно после коммутации

Ll (0+)+ %2 (0+) = (Lib-2) 1 (0+)/2 =

=1? £V[2 ih+L) R

меньше, чем энергия, запасенная в индуктивности L до коммутации:

Ll (0 )--=-ill (0 )/2 = i., £V(2/?),

причем разность между этими величинами равна энергии коммутационных потерь. Рассмотренная коммутация может быть сделана корректной, если при анализе принять во внимание конечное время коммутации, применить более точные модели индуктивных катушек, содержащие не только сопротивления потерь, но и паразитные емкости, и учесть явления, имеюш,ие место в искре и.ги дцге между контактами. Разумеется, учет этих явлений существенно усложняет анализ.

Общий подход к анализу переходных процессов

Задача анализа переходных процессов заключается в общем случае в определении мгновенных значений токов и напряжений всех или части ветвей электрической цепи в произвольный момент времени после коммутации. Для этого необходимо найти общее решение основной системы уравнений электрического равновесия цепи или системы уравнений электрического равновесия, составленной любым другим способом, при /> 0. Исключая из системы уравнений все неизвестные величины, кроме одной, получают дифференциальное уравнение цепи, составленное относительно этой величины. Таким образом, задача анализа переходных процессов может быть сведена к решению дифференциального уравнения цепи при > 0. В частности, задача анализа переходных процессов в линейной инвариантной во времени цепи с сосредоточенными параметрами v-ro порядка сводится к нахождению об-

щего решения линейного неоднородного дифференциального уравнения \-го порядка вт1да (1.61).

Общее решение такого уравнения содержит v произвольных постоянных, для нахождения которых необходимо задать значения искомой функции у и ее V - 1 первых производных в начальный момент времени после коммутации, т. е. при t = 0+. Эти величины определяют с помощью законов коммутации на основании анализа процессов, имеющих место в рассматриваемой цепи перед коммутацией. В результате анализа цепи до коммутации рассчитывают значения токов всех индуктивностей и напряжения всех емкостей в момент времени, непосредственно предшествующий коммутации. Далее, используя законы коммутации (в более общем случае - принцип непрерывности потокосцепления и электрического заряда цепи), находят значения токов индуктивностей и напряжений емкостей в начальный момент времени после коммутации. Очевидно, что для определения v начальных условий требуется применить законы коммутации к v независимо включенным реактивным элементам, т. е. к реактивным элементам, включенным таким образом, что их энергетическое состояние может быть задано независимо. Следовательно, порядок сложности цепи, равный порядку дифференциального уравнения цепи v, определяется числом независимо включенных реактивных элементов. Совокупность начальных значений токов независимо включенных индуктивностей и напряжений независимо включенных емкостей представляет собой независимые начальные условия цепи. Используя независимые начальные условия и уравнения электрического равновесия цепи после коммутации, находят зависимые начальные условия, т. е. значения токов и напряжений любых ветвей и их производных в момент времени / = 0+.

Если энергия, запасенная в цепи в момент времени, непосредственно предшествующий коммутации, равна нулю, то говорят, что цепь, анализируется при нулевых начальных услови я*х. Если начальный запас энергии не равен нулю, то цепь анализируется при ненулевых начальных условиях (в первом случае все независимые начальные условия равны нулю, во втором случае хотя бы одно из них имеет ненулевое значение).

Следует обратить внимание на то, что независимые начальные условия, а следовательно, токи и напряжения ветвей цепи после коммутации определяются исходя из энергетического состояния цепи только в момент времени, непосредственно предшествуюиий коммутации (t = 0 ), и не зависит от характера процессов, имеющих место в рассматриваемой цепи до коммутации (при t-<0).

Определение порядка сложности цепи

В некоторых случаях порядок сложности электрической цепи v бывает желательно выяснить еще до составления уравнений электрического равновесия. Очевидно, что значение v не может превышать общего числа реактивных элементов цепи pLc- В связи с тем что последовательно или параллельно включенные реактивные элементы од-

Qio типа не являются энергетически независимыми, при подсчете dlc необходимо объединять такие элементы и заменять их эквива-дентным элементом соответствующего типа.

Если в цепи имеется так называемый емкостный контур, е. контур, образованный только емкостями и, может быть, независимыми источниками напряжения, то напряжение любой из емкостей такого контура выражают через напряжения других емкостей с помощью уравнения баланса напряжений, составленного для данного емкостного контура. Таким образом, наличие в цепи емкостного контура уменьшает на единицу число независимо включенных емкостей и снижает порядок сложности цепи.

rv-v-4

«2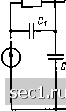

Рис. 6.3. К примеру 6.3

Число независимо включенных индуктивностей снижается при наличии в цепи так называемого индуктивного сечения, т. е. сечения, в которое входят только индуктивности, и, может быть, независимые источники тока. Частным случаем индуктивного сечения является индуктивный узел (узел, к которому подключены только индуктивности и независимые источники тока). Ток, а следовательно, и энергия любой из индуктивностей, входящей в индуктивное сечение, могут быть выражены через токи других индуктивностей на основании уравнений баланса токов, составленного для данного сечения.

Если в состав цепи входит несколько емкостных контуров или индуктивных сечений, то при оценке числа независимо включенных реактивных элементов учитывают только независимые емкостные контуры и,независимые индуктивные Сечения, т. е. такие контуры и сечения, уравнения баланса напряжений и токов которых независимы.

Таким образом, порядок сложности линейной цепи, составленной только из идеализированных пассивных элементов и независимых Источников тока или напряжения:

V = PLC - «ек - Qv

(6.4)

Plc - общее число реактивных элементов; - число независимых емкостных контуров; („с - члсло независимых индуктивных сечений.