3. Составление дифференциального урав-jjgHHfl цепи после коммутации (при 0). Дифференциальное уравнение цепи получают из системы уравнений электрического равновесия цепи, составленной любым методом, путем исключения всех неизвестных величин, кроме одной, представляющей собой ток или напряжение какой-либо ветви.

4. Анализ установившегося процесса в цепи после коммутации (при t-i- ос). В результате анализа установившегося процесса в цепи после коммутации находят принужденную составляющую реакции цепи (частное решение дифференциального уравнения цепи).

5. Определение свободной составляющей реакции цепи. На этом этапе составляют характеристическое уравнение цепи, находят его корни и определяют общий вид свободной составляющей реакции цепи (общее решение однородного дифференциального уравнения, соответствующего дифференциальному уравнению цепи после коммутации).

6. Нахождение общего вида реакции цепи. Общий вид реакции цепи (общее решение дифференциального уравнения цепи) находят путем суммирования свободной и принужденных составляющих реакции цепи.

7. Определение постоянных интегрирования. Постоянные интегрирования находят по зависимым начальным условиям (значениям искомых токов или напряжений и их v - 1 первых производных в начальный момент времени после коммутации). Для определения зависимых начальных условий используют независимые начальные условия и уравнения электрического равновесия цепи после коммутации.

8. Определение реакции цепи, соответствующей заданным начальным условиям. Подставляя постоянные интегрирования в общее решение дифференциального уравнения цепи после коммутации, находят частное решение дифференциального уравнения, соответствующее заданным начальным условиям, т. е. искомый ток или напряжение одной из ветвей при > 0.

Переходные процессы в последовательной /?С-цепи при скачкообразном изменении э. д. с.

Рассмотрим переходные процессы в последователоной 7?С-цепи (рис. 6.4, а) при скачкообразном изменении э. д. с. идеализированного источника постоянного напряжения

1 при / > 0.

Такое изменение э. д. с. источника напряжения происходит напри-**ер, когда в цепи, схема которой приведена на рис. 6.4, б, ключ S в Момент времени = О перебрасывают из положения / в положение 2.

Очевидно, что в момент времени, непосредственно предшествовавший коммутации, напряжение на емкости равнялось напряжению на зажимах источника энергии при t <.0 (предполагается, что до коммутации цепь находилась в установившемся режиме). Используя второй закон коммутации, находим единственное независимое начальное условие

"с (0.) = Uc (0-) = £i. (6.9)

Дифференциальное уравнение рассматриваемой цепи можно составить относительно любой из неизвестных величин (напряжения на сопротивлении Ыд, напряжения на емкости Uc, тока сопротивления

Bit) Вг

С) e(i)

£2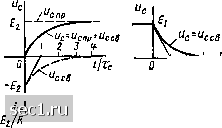

i Z Z Ч- t[Tc 0

t 2 3 U-

he:::

,0 i 2 3 4t/Zg

•EilR

ol г 3 и

/ 2 J 4<До

Рис. 6.4. К исследованию переходных процессов при скачкообразном изменении э. д. с. в последовательной НС-цепи:

а, б -схемы цепи; в -£i = 0; г - £ = 0; д ~ Ei>Et>0

in, тока емкости ic), однако, учитывая, что для данной цепи известно начальное значение напряжения на емкости, целесообразно составить уравнение относительно этого напряжения.

Исключая из основной системы уравнений электрического равновесия цепи при t 0

Ur +Uc==--En; ic-C

ic = »я »; "r = 4

все неизвестные величины, кроме и с, получаем

Напряжение на емкости при t О представим в виде суммы принужденной и свободной составляющих

«с = «Спр + «сев. (6.10)

Очевидно, что с течением времени после коммутации в цепи должен установиться режим постоянного тока, причем установившееся значение тока емкости будет равно нулю (сопротивление емкости постоянному току бесконечно велико), а установившееся значение напряжения на емкости - напряжению источника энергии после коммутации. Таким образом, принужденная составляющая напряжения на емкости

"спр = £2- (6.11)

Характеристическое уравнение цепи

RCp +1=0

имеет единственный корень

р, = -1/ (RC) = -1/тс,

где Тс RC- постоянная времени последовательной RC-uem, поэтому свободная составляющая напряжения на емкости и сов содержит один экспоненциальный член

мссв=Ле-=Л1е-Ч (6.12)

Используя выражения (6.10), (6.11) и (6.12), находим напряжение на емкости после коммутации при произвольных начальных условиях

ис=-Е, + А,е-". (6.13)

Для определения постоянной интегрирования Ai воспользуемся независимым начальным условием (6.9). Полагая в (6.13) / - О, и, = = Uc (0+) = El, получаем Е Е i- Ai, откуда А = Еу - Е.

Таким образом, при заданных начальных условиях напряжение на емкости после коммутации {t 0) определяется выражением

Uc = E2-~{E-Ei)&-*. (6.14)

Зависимость напряжения на емкости от времени при различных соотношениях между Е и Е показана на рис. 6.4, в-д. Здесь же показана зависимость от времени тока емкости ic, которая при О определяется путем дифференцирования выражения (6.14) по времени и умножения результата на С:

i,.-Ae-" (6.16)