Как видно из рисунка, в начальный момент после коммутации напряжение на емкости сохраняет то же значение, что и до коммутации, а затем плавно изменяется, стремясь в пределе к новому установившемуся значению. Ток емкости в начальный момент скачком изменяется от нуля до начального значения:

fc (Он.) = (£2 - (6.16)

а затем плавно уменьшается, стремясь в пределе к нулю. В связи с тем что установившееся значение тока емкости до и после коммутации равно нулю, ток рассматриваемой цепи содержит только свободную составляющую.

Анализ выражения (6.16) показывает, что значение тока емкости ic (0+) численно равно постоянному току, который протекал бы в цепи после коммутации, если бы емкость С была заменена идеальным источником напряжения э. д. с. Следовательно, в начальный момент времени после коммутации емкость ведет себя подобно источнику напряжения, э. д. с. которого равна начальному значению напряжения на емкости. Если начальное значение напряжения на емкости равно нулю, то в начальный момент после коммутации ветвь с емкостью можно считать короткозамкнутой, т. е. сопротивление емкости равно нулю.

Далее (см. пример 6.4) будет показано, что в начальный момент времени после коммутации индуктивность ведет себя подобно источнику тока, ток которого равен начальному значению тока через индуктивность. При fi, (0 ) = О ветвь с индуктивностью в начальный момент времени можно считать разомкнутой, т. е. сопротивление индуктивности при t = 0+ имеет бесконечно большое значение.

Как видно из выражений (6.12) и (6.15), скорость затухания свободных составляющих тока и напряжения емкости не зависит от Аа-чения э. д. с. идеализированного источника напряжения до и после коммутации, а определяется только постоянной времени цепи Хс, которая численно равна промежутку времени, в течение которого свободные составляющие тока и напряжения уменьшаются в е » 2,718 раз. Можно показать, что при любом / О

"с св

d"ccJdt

Таким образом, постоянная времени рассматриваемой цепи численно равна длине подкасательной к кривой «Сев или f сев при любом значении / О, т. е. длине отрезка временной оси, заключенного между какой-либо точкой t = /1 О и точкой пересечения временной оси касательной, проведенной к кривой «сев или tсев в точке «сев (i) или ffcH (1) Для определения постоянной времени цепи касательную к кривым «геи или «сн наиболсе удобно проводить при 1 == 0. В этом случае она пересекает ось времени в точке / - (рис. 6.4, в-д).

Чем больше постоянная времени цепи, тем медленнее затухают свободные составляющие токов и напряжений и, следовательно, токи и напряжения цепи медленнее приближаются к установившимся значениям.

Теоретически npouecc установления нового режима длится бесконечно долго, однако, учитывая, что к моменту времени, равному 4тс после коммутации, свободные составляющие уменьшаются да уровня менее 0,02 от начального значения, переходные процессы в цепи можно считать практически закончившимися через промежуток времени (4-5)Тс после коммутации.

Подключение к последовательной L-цепи источника гармонического напряжения

Рассмотрим переходные процессы в последовательной iL-цепи, содержащей идеализированный источник, э. д. с. которого е (t) изменяется во времени по закону

О при / < 0;

jG cos (w/ + i3) при/>0.

(6.17)

Временная диаграмма е (t) при i)>0 приведена на рис. 6.5, а. В этом случае ток индуктивности в момент времени, непосредственно предшествующий коммутации, II (0-) = 0.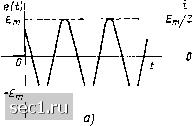

-и-----и----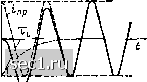

Рис. 6.5, К нсследованню переходных процессов при включении источника гармонического напряжении в последовательную

/?1-цепь

Дифференциальное уравнение цепи, составленное относительно тока i = II, при t О имее- вид

L- + Ш = Ет cos + (б.18>

Принужденная составляющая тока может быть найдена с помощью метода комплексных амплитуд

inp соз((о/+г{5-ф),

где Z --- У -]- (o)L)*, ф = arctg (aL/R) -»модуль и аргумент комплексного входного сопротивления рассматриваемой цепи. Характеристическое уравнение цепи

Lp + R = 0

имеет единственный корень /?i = -RIL, поэтому свободная составляющая тока содержит один экспоненциальный член

где Ti, = LIR -- постоянная времени последовательной iL-цепи.

Суммируя свободную и принужденную составляющие, находим общее решение дифференциального уравнения цепи (6.18) после коммутации:

I cos ((й + г1з-ф)--Л . (6.19)

Для определения постоянной интегрирования Ai воспользуемся первым законом коммутации, в соответствии с которым начальное значение тока рассматриваемой цепи должно равняться нулю:

t(0+)=iL(0+)-ii.(0 )=0. (6.20)

-f = О, откуда

Подставляя (6.20) в выражение (6.19), получаем cos (f - ф) +

Л= cos(i) -ф). (6.21)

с учетом (6.21) выражение для тока рассматриваемой цепи после коммутации принимает вид

i cos ((1) + г;-ф) - 3». [cos (г1з -ф)] е~".

Характер переходных процессов зависит от соотношения между начальной фазой f э. д. с. идеализированного источника напряжения и аргументом ф входного сопротивления цепи. Если гз выбирают таким образом, что начальные значения принужденной i„p (0+) и свободной св (Ое) составляющих равны нулю (ij) = ф ifc Jt/2), то свободная составляющая тока тождественно равна нулю. Переходные процессы в цени в этом случае отсутствуют, т. е. установившийся режим наступает сразу же после коммутации. При ij; = ф или я; ф ± л начальные значения свободной и принужденной составляющих максимальны, и отличие в форме кривых i = i (t) и i„p -= i„p (t) выражено наиболее резко (рис. 6.5, б).

Как и для последовательной RC-цепи, скорость затухания свободной составляющей тока рассматриваемой цепи не зависит от характера внешнего воздействия, а определяется только постоянной времени Т/ . За промежуток времени t свободная составляющая тока уменьигается в е раз и к моменту времени / (4 -г 5)xi после коммутации переходные процессы в цени можно считать практически закончившимися.