Подключение к последовательной RLC-u.en4 источника постоянного напряжения *

Последовательная iLC-цепь содержит два независимо включенных реактивных элемента, поэтому процессы в ней описываются дифференциальным уравнением второго порядка, а для определения постоянных интегрирования необходимо задать два независимых начальных условия. Если э. д. с. идеального источника напряжения изменяется во времени по закону

,() ( О при/<0;

1 Е = const при t 0,

то независимые начальные условия цепи имеют нулевые значения

Uc (0J = Uc (0 ) = 0; i, (0+) = 1д (0-) - 0. (6.22)

Составим уравнение электрического равновесия цепи по методу токов ветвей

E- + Ri + Uc (О +) + -1 j id/ = £. (6.23)

Дифференцируя правую и левую части (6.23), получаем дифференциальное уравнение рассматриваемой цепи после коммутации

Для определения единственного решения этого уравнения, соответствующего заданному режиму работы цепи до коммутации, необходимо определить начальные значения тока цепи и его первой производной по времени. Начальное значение тока цепи совпадает с начальным значением тока индуктивности

i (О J i,. (0+) = О, (6.25)

а начальное значение первой производной тока цепи по времени может быть найдено с использованием независимых начальных условий (6.22) и уравнения электрического равновесия цепи (6.23) при /= 0 =0;

= ~ . (6.26)

В связи с тем что установившееся значение тока этой цепи после коммутации равно нулю,ток при / > О содержит только свободную составляющую: i --- tcB •

*) Приведенные здесь результаты легко использовать для анализа переходных процессов в одиночном колебательном контуре, причем в связи с тем, что свободные составляющие тока и напряжения контура определяются при выключенных источниках энергии, нетрудно заключить, что характер свободных процессов в одиночном колебательном контуре не зависит от способа подключения контура к источнику энергии, т. е. от того, является данный одиночный контур «последовательным» или «параллельным».

Характеристическое уравнение последовательной RLC-цепя

Lp+Rp+l/C=0 (6.27)

lecT два корня

(6.28)

ае б = R/{2L) - коэффициент затухания; = \IYLC - резонанс-ая частота цепи. В зависимости от соотношения между величинами )о и б, или, что то же самое, в зависимости от добротности цепи,

0=-£-= -l/" А =5aiL.

R R V С R 2S

орни характеристического уравнения (6.27) могут быть вещественны-1и различными, комплексно-сопряженными или вещественными динаковыми (кратными). Рассмотрим каждый из этих случаев.

Вещественные различные корни. При малой (обротности последовательной RLC-тпн (Q<; 1/2, т.е. R:>2p и ) > ©о) характеристическое уравнение (6.27) имеет два различных ве-цественных отрицательных корня, а выражение для тока цепи после <оммутации {t > 0) содержит два экспоненциальных члена:

»==гев=Ле"--Ле=. (6.29)

Дифференцируя правую и левую части выражения (6.29) dlldt = pAid* + /asC* и используя зависимые начальные условия (6.25), (6.26), составляем уравнения для определения постоянных интегрирования Ai и Ач. Ai + А = 0; рА + р%А = ElL, откуда

А •

Z, (Pl-Рг) 2L Уб--(og •

С учетом (6.30) выражение для тока цепи после ком.мутации принимает вид

/ =- (е" - еР

Расположение корней pi, р характеристического уравнения в плоскости комплексного переменного р и зависимость нормированного тока рассматриваемой цепи от времени

1 2y-b)g •ep.< ep,f 7(1) -Ч2)

приведены на рис. 6.6, а. Переходной процесс в цепи носит апериодический (неколебательный) характер, причем вследствие того, что \p\\<t. 1/721) вторая составляющая нормированного тока цепи затухает быстрее, чем первая j().

Комплексно-сопряженные ки>... ...

добротности последовательной /LC-цепи (Q > 1/2, т. е. /? < 2р и 6 < Юо) характеристическое уравнение (6.27) имеет два комплексно-сопряженных корня

/1,2 = -6 ± /(йсв,

где «йсв = vMo - - частота свободных колебаний в цепи (смысл этого понятия будет ясен из последующего изложения). Ток цепи после коммутации, как и в предыдущем случае, определяется выражением

со„

о Re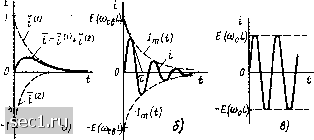

Рис. 6.6. Расположение корней характеристического уравнения в плоскости комплексного переменного и зависимость свободной составляющей тока последовательной RLC-ЦйШ от времени для: я -б>а)о; б - 6<соо; в - 6-0; г -

(6.29), которое после нахождения постоянных интегрирования = = Е1{]2(йсвЦ, Ai - - £/(/2(0св) может быть с учетом соотношения

есв е~<=»

= sin (й„„ t

преобразовано к виду Е

i =

wcb L

е-« sin Шов =/т (О cos («й,в /-я/2).

где (/) = £е-«/((ОевЬ).

Таким образом, при включении в последовательную iLC-цепь с высокой добротностью идеального источника постоянного напряжения переходные процессы в ней имеют колебательный харак- р. Ток цепи представляет собой затухающую гармоническую функцию, амплитуда которой экспоненциально уменьшается во времени. Колебательный характер переходного процесса в цепи связан с перио-

як 565