Таким образом, в последовательной iLC-цепи, удовлетворяющей принятым допущениям, свободная составляющая тока является затухающей гармонической функцией времени. В начальный момент времени амплитуда свободной составляющей тока равна амплитуде принужденной составляющей, а затем уменьшается по экспоненциальному закону. Через промежуток времени, равный (4--5) т после коммутации, амплитуда свободной составляющей становится пренебрежительно малой по сравнению с амплитудой принужденной составляющей, и переходной процесс в цепи можно считать практически закончившимся.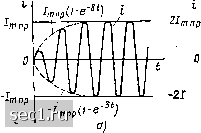

I \ I \

-21„пр§г.л-2-*

Рис. 6.7. Зависимость тока последовательной /?/,С-цепи от времени при включении источника гармонического напряжения:

Ток цепи после коммутации равен сумме свободной и принужденной составляющих:

г = /тпр sin (со/ - ф) - /тир в"* sin ((йо/ - ф). (6.42)

Если частота внешнего воздействия оо в точности совпадает с резонансной частотой цепи ooq, то входное сопротивление цепи имеет чисто резистивный характер ((f = 0) и выражение (6.42) принимает вид (рис. 6.7, а)

i = /тнр (1 - е-б) sin w,t. (6.43)

Как видно из рисунка, амплитуда тока цепи при оо = сло плавно увеличивается во времени, стремясь в пределе к установившемуся значению /тпр- Ни при каких значениях / амплитуда тока после коммутации не превышает этого значения.

При включении в последовательную RLC-тпъ источника гармонического напряжения, частота которого близка к резонансной, но не равна ей, в цепи наблюдаются биения, заключающиеся в периодическом увеличении амплитуды тока или напряжения до значения, значительно превышающего амплитуду принужденной составляющей (рис. 6.7, б). Если пренебречь затуханием свободной составляющей тока (6 = 0), то из выражения (6.42) получаем

1=2/

т пр

sin -

0)-СОп

(6.44)

Как видно из этого выражения, ток цепи имеет частоту, близкую к резонансной, а амплитуда тока (О медленно изменяется во времени:

/m(0 = 2/m„psin-:= (6.45)

причем максимальное значение тока в переходном режиме в два раза превышает амплитуду принужденной составляющей..

Возникновение биений при включении источника гармонического напряжения в последовательную iLC-цепь объ.сняется тем, что вследствие несовпадения частот внешнего воздействия и свободных колебаний фазовые соотношения между свободной и принужденной составляющими тока непрерывно изменяются, а разность мгновенных фаз этих колебаний (со - (Oo)t линейно нарастает во времени. В те моменты времени, когда разность мгновенных фаз будет равна 2кл, где й= О, 1, 2, .... сумма мгновенных значений /св и fnp будет максимальна, а в те моменты времени, когда разность фаз будет равна (2ft-f 1)я, - минимальна. Частотой биений называют частоту повторения максимумов огибающей тока (6.45). Угловая частота биений, таким образом, равна абсолютному значению разности угловых частот свободной и принужденной составляющей

В реальных колебательных контурах коэффициент затухания б имеет малое, но конечное значение. Свободная составляющая тока в таких контурах экспоненциально уменьшается во времени, а биения носят затухающий характер.

§ 6.3. операторный метод анализа переходных процессов

Преобразование Лапласа и его применение к решению дифференциальных уравнений

Классический метод анализа переходных процессов применяют в основном тогда, когда исследуемая цепь имеет невысокий порядок сложности, а внешнее воздействие на нее после коммутации является гармонической функцией времени либо постоянно. Если внешнее воздействие на цепь после коммутации имеет более сложный характер, то определение принужденной составляющей реакции цепи существенно затруднено, а при повышении порядка цепи усложняется определение постоянных интегрирования. Значительно большие возможности пред--ставляет операторный метод анализа переходных процессов, основанный на применении преобразования Лапласа. Подобно ранее рассмотренному методу комплексных амплитуд, операторный метод относится к символическим методам, в которых операции над функциями времени заменяются операциями над их символами (изображениями). Взаимное соответствие между функцией времени а (О и ее

изображением А (р) ъ операторном методе устанавливается с помощью прямого

А{р)=Ь[а (t)] = г e-Pt а (t) dt (6.46)

ИЛИ обратного

a(0=L-H(p)]= J eA{p)dp (6.47)

Преобразований Лапласа и указывается знаком соответствия

а (О = Л (р).

Функция А (р) называется операторным изображением функции а (t) или изображением функции р. (t) по Лапласу. Исходная функция времени а (t) по отношению к своему операторному изображению является оригиналом. Комплексное число р будем называть оператором преобразования Лапласа или комплексной частотой (смысл последнего понятия будет пояснен в следующем параграфе).

Из курса высшей математики известно, что для функций а (t), равных нулю при / < О, интегрируемых при t > О и удовлетворяющих неравенству

1 а (О I < К е"»,

где АГ и (j„ - некоторые постоянные числа, интеграл (6.46) абсолютно сходится при Re (р) > а„. Изображение А (р) в полуплоскости Re (р) > Oq является аналитической функцией р, которая стремится к нулю при Re(p)->-oo. На практике к интегрированию по формулам (6.46), (6.47) приходится прибегать-сравнительно редко, так как для большинства часто употребляемых функций разработаны таблицы прямого и обратного преобразований Лапласа [6, 7]. Операторные изображения некоторых функций приведены в приложении 1. Следует иметь в виду, что в ряде справочников, в частности в [6], приведены таблицы преобразовании Карсона-Хевисайда

Ау (P) = pf е-а(0 dtpAip),

которое отличается от преобразования Лапласа только наличием множителя р.

Напомним некоторые свойства преобразования Лапласа.

Изображение по Лапласу постоянной величины К равно этой величине, деленной на р:

К = К/р. (6.48>

Умножение функции времени а (t) на постоянное число К соответствует умножению на это же число ее изображения:

Ка ii) = К А ip). (6.49>

Изображение суммы функций времени равно сумме изображений этих функций:

2 at (О = i Л, (р), (6.50)

где Oi (t) = Ai (р).