Ur(P} IJZr{PJ?R

Рис. 6.8. Операторная схема замещения сопротивления

им операторным входным сопротивлением или операторной входной проводимостью, а токи и напряжения на его зажимах - их операторными изображениями. Если в рамках решаемой задачи двухполюсник не находится при нулевых начальных условиях, то его операторная эквивалентная схема должна содержать независимый источник тока или напряжения, характеризующий начальные запасы энергии в цепи.

Рассмотрим операторные компонентные уравнения и операторные схемы замещения идеализированных пассивных двухполюсников.

Сопротивление. Соотношения между мгновенными значениями тока и напряжения на зажимах сопротивления устанавливаются выражениями (1.9), (1.10): Ыд =

= RiR, Ir = Gur.

Учитывая, что умножению функции времени на постоянное число соответствует умножение изображения функции на это же число (6.49), для получения компонентных уравнений сопротивления в операторной форме достаточно в выражениях (1.9), (1.10) заменить мгновенные значения токов и напряжений их операторными изображениями

Ur (р) = RIr ip); (6.63)

Ir (р) = GUn (р). (6.64)

Подставляя соотношения (6.63), (6.64) в (6.61), (6.62), находим выражения для операторного входного сопротивления и операторной входной проводимости

Zr (р) = R; Yu (P)-G MR. (6.65)

Операторная эквивалентная схема сопротивления приведена на рис. 6.8.

Емкость. Напряжение и ток емкости связаны соотношениями (1.13), (1.16):

; uc = Uc{0)-\-~.icdt.

Используя теоремы дифференцирования (6.52) и интегрирования (6.53), получаем

1с {р)-=р CUc{p)-Cuc{0);

Ucip)-

«c(0)

Icip).

(6.66) (6.67)

P pc

Операторные компонентные уравнения емкости (6.66) и (6.67) являются равносильными и могут быть получены одно из другого. При нулевых начальных условиях (и с (0) = 0) они принимают вид

1с (р) = pCUc (р)\ и, (р) = /с ipVipQ.

Таким образом, операторное входное сопротивление Zc {р) w- операторная входная проводимость емкости Yг; (р) определяются выражениями

Zc (Р) = 1/(рС); Ус (Р) = рС. (6.68)

Операторным компонентным уравнениям (6.66) и (6.67) соответствуют параллельная и последовательная схемы замещения емкости (рис. 6.9, а, б), содержащие независимый источник тока Cuc (0) или напряжения и с (0)/р. При нулевых начальных условиях независимые источники тока или напряжения, характеризующие начальный запас энергии в емкости, выключаются, и в операторной эквивалентной схе-

1с (Р)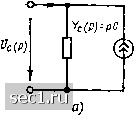

Ш с(0)/р

си,(а)

в)

Рис. 6.9. Операторные схемы замещения емкости: а - параллельная при ненулевых начальных условиях; б - последовательная при ненулевых начальных условиях; в - при нулевых начальных условиях *

ме емкости остается только один элемент - операторное входное сопротивление или операторная входная проводимость емкости (рис. 6.9, в).

Индуктивность. Мгновенные значения тока и напряжения индуктивности связаны между собой соотношениями (1.22) и (1.23):

Ui.==L-; ix. = it(0)+--J«L.

Применяя к этим выражениям теоремы дифференцирования (6.52) и интегрирования (6.53), получаем компонентные уравнения индуктивности в операторной форме:

Uip) = pLhip)- LiiO); (6.69)

Il ip) = iL (0)/p + i/b ipVipL)- (6.70)

Уравнения (6.69), (6.70) равносильные и могут быть получены одно из другого с помощью элементарных преобразований. Используя их, определяем комплексное входное сопротивление и комплексную входную проводимость индуктивности

Zr. (р) = pL; Yr. (р) = l/ipL) (6.71)

и строим ее последовательную и параллельную схемы замещения (рис. 6.10, а, б). Как и операторные схемы замещения емкости, операторные схемы замещения индуктивности содержат независимый ис-

точник напряжения Lti, (0) или тока /х, (0)/р, характеризующий начальный запас энергии в индуктивности. Операторная эквивалентная схема индуктивности при нулевых начальных условиях приведена на рис. 6.10, в.

Анализируя полученные результаты, нетрудно установить, что выражения для операторных входных сопротивлений (проводимостей) идеализированных пассивных элементов имеют такую же структуру, как и выражения для комплексных входных сопротивлений (проводимостей) этих же элементов, и могут быть получены одно из другого путем замены /ы иа р.

Аналогичным образом может быть получено выражение для операторного входного сопротивления (проводимости) произвольного линейного двухполюсника, составленного из идеализированных пассивных

kiP)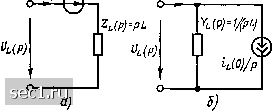

hiP)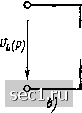

\\4iP)-pL

Рис. 6.10. Операторные схемы замещения индуктивности: а - последовательная при ненулевых начальных условиях; б - параллельная при ненулевых начальных условиях; в - при нулевых начальных условиях

элементов. Поэтому для преобразования операторных схем замещения линейных пассивных двухполюсников при нулевых начальных условиях можно использовать все рассмотренные ранее (см. гл. 2) правила преобразования линейных пассивных цепей при гармоническом воздействии, а для преобразования операторных схем замещения тех же участков цепей при ненулевых начальных условиях - правила преобразования активных двухполюсников. В частности, последовательная и параллельная схемы замещения емкости или индуктивности могут быть преобразованы одна в другую с помощью рассмотренных ранее (см. гл. 2) приемов преобразования активных двухполюсников.

Используя операторные эквивалентные схемы идеализированных пассивных элементов, можно получить операторную эквивалентнук» схему произвольного участка линейной цепи или всей цепи в целом. С этой целью каждый идеализированный пассивный элемент, изображенный на эквивалентной схеме цепи для мгновенных значений, должен быть заменен оперйторной эквивалентной схемой, а токи к напряжения идеализированных источников тока или напряжения - представлены операторными изображениями соответствующих функций.

Операторная эквивалентная схема цепн имеет такую же структуру, как и эквивалентная схема цепн для мгновенных значений, но содержит дополнительные независимые источники энергии, определяющие запасы энергии цепн в момент времени, непосредственно предшествовавший коммутации.