Используя операторную схему замещения цепи, можно с помощью любого из известных методов сформировать систему уравнений ее электрического равновесия в операторной форме, которая будет равносильна основной системе уравнений электрического равновесия цепи после коммутации.

В связи с тем что операторная схема замещения цепи может быть построена непосредственно по эквивалентной схеме цепи для мгновенных значений, этап формирования дифференциальных уравнений цепи может быть исключен. Метод анализа переходных процессов в линейных цепях, основанный на формировании операторных уравнений электрического равновесия цепей по их операторным эквивалентным схемам, получил название операторного метода анализа переходных процессов. Этот метод представляет собой дальнейшее развитие операторного метода решения дифференциальных уравнений и позволяет анализировать процессы в цепи после коммутаций, минуя этап формирования уравнений электрического равновесия цепи для мгновенных значений токов и напряжений.

Общая схема применения метода

Наметим основные этапы анализа переходных процессов в линейных цепях с помощью операторного метода.

1. Анализ цепи до коммутации и определение независимых начальных условий. Выполняются так же, как и при использовании классического метода анализа переходных процессов.

2. Составление операторной эквивалентной схемы цепи после коммутации. Составление оператошой эквивалентной схемы цепи производится непосредственно по эквивалентной схеме цепи для мгновенных значений путем замены каждого идеализированного пассивного элемента его операторной схемой замещения и представления токов и напряжений идеализированных источников тока или напряжения их операторными изображениями.

3. Составление уравнений электрического равновесия цепи в операторной форм е. Система . уравнений электрического равновесия цепи в операторной форме может быть сформирована любым из рассмотренных в гл. 4 методов непосредственно по операторной схеме замещения цепи.

4. Решение уравнений электрического равновесия цепи относительно изображений искомых токов и напряжений. Может производиться любым методом, в том числе путем использования рассмотренного ранее метода сигнальных графов.

5. Определение оригиналов искомых то-кови напряжений. Как правило, производится путем применения таблиц обратного преобразования Лапласа [6] и использования основных свойств преобразования Лапласа. Если изображение инте-

ресующей функции представляет собой отношение двух полиномов р, для выполнения обратного преобразования Лапласа можно воспользоваться теоремой разложения.

• ••••

Пример 6.4. Для цепи, схема которой приведена на рис. 6.11, а, найдем зависимость тока и напряжения индуктивности ig, U3 от времени при t 0. Э.д.с. идеализированного источника постоянного напряжения е (t) при t - О скачком изменяется от Ej до Е.

г £1 при / < 0; . £2 при > О •

e(i) =

Анализируя процессы в цепи до коммутации, находим начальное значение тока индуктивности

Для построения операторной эквивалентной схемы цепи после коммутации (рис. 6.11, б) заменяем все идеализированные пассивные элементы их операторными схемами замещения, а э. д. с. идеализированного источника напряжения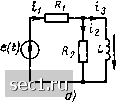

Рис. 6.11. к примеру 6.4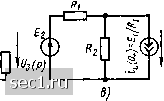

- операторной э.д.с, Е (р) = Ejp. Используя метод контурных токов, составляем систему уравнений электрического равновесия цепи в операторной форме

(Ri + R2) hi (Р) - R2I22 (Р) Е/р; - RIn (Р) + + pL) In (Р) = LEiRi,

где /,1 (р) = 1 (р) == i\; /22 (р) = /3 <р) Ф «3. Решая эту систему уравнений, находим операторные изображения искомого тюка

/з (Р) = [R1R2E2 + pL (Ri + «2) EVipRi IPL (Ri + R2) + R1R2]} и напряжения

(Уз (р) = pL/з (р) - EL/Ri \LR (£j - £,)]/[pL (R + R) + RR].

Преобразуем получениые выражения к такому виду, чтобы для выполнения обратного преобразования Лапласа можно было непосредственно воспользоваться таблицами, приведенными в приложении 1:

/з (Р) -

{P+Ri Ri/IL {Ri-hR2)\} Ri 1 R2E2

P {P-Ri R2l[L (Ri + R-,)]} L (Ry-R)

{p + RiR2/[L (Ri + R,)]} Rt + R2

Учитывая, что + a) = e~°" и l/[p (p + a)] = (1 - eполучаем выражения для искомых тока и напряжения индуктивности при / > О

JE1 е-/Ч - (1-е-/) = -- e-/ Ну Rl Rl Rl

R2 {E,-Ei) Ri + Ri

где X = (Rl + R) L/iRiR) - постоянная времени рассматриваемой цепи.

Как видно из полученных соотношений, в начальный момент времени ток индуктивности сохраняет то же значение, что и до коммутации (0) = EjR, а затем плавно изменяется, стремясь в пределе к ERi- Напряжение индуктивности в начальный момент времени скачком изменяется от нуля до и (0+) = = /?2 (2 - i) (Rl + Ri), а затем плавно уменьшается до нуля.

Нетрудно заметить, что в начальный момент времени (i = 0+) ток и напряжение индуктивности принимают такие значения, которые они имели бы в случае, если индуктивность была заменена идеализированным источником тока (рис. 6.11, в), ток которого равен (3 (0) = EilRi. Таким образом, в начальный момент после коммутации индуктивность ведет себя подобно идеализированному источнику тока (при нулевых начальных условиях ток этого источника равен нулю, и, следовательно, ветвь, содержащую индуктивность, в начальный момент времени можно считать разомкнутой).

§ 6.4. ОПЕРАТОРНЫЕ ХАРАКТЕРИСТИКИ В.Об, $6? ЛИНЕЙНЫХ ЦЕПЕЙ " - , 9 - в **SiO

Реакция цепи на экспоненциальное воздействие

Выясним, какой физический смысл имеет оператор р, входящий в выражения для операторных сопротивлений и проводимостей. С этой целью найдем реакцию цепи на экспоненциальное внешнее воздействие

а(/) = Ле, (6.72)

где Л и S - некоторые комплексные числа.

Коэффициент А = Аел имеет размерность внешнего воздействия и называется обобщенной комплексной амплитудой, величина s = а -f /ю - имеет размерность с-" и называется обобщенной (комплексной) частотой.

Заметим, что многие встречающиеся на практике внешние воздействия можно рассматривать как частный случай экспоненциального воздействия или как сумму некоторого их количества. Действительно, при Im Л = Ims = О выражение (6.72) описывает экспоненциально затухающее (а<С 0), экспоненциально нарастающее (а>> 0) или неизменное (а = 0) внешнее воздействие. Сумма экспоненциальных воздействий с комплексно-сопряженными амплитудами и комплексно-сопряженными частотами представляет собой гармоническое колебание

а(/) = Ле- -fie =Леае(+*) + е-"("+*)1 =

= 24e°cos((i)/-f я;л), (6.73)