(условие появления субгармоник). В других режимах ра-боты НПЧ с ОМ в кривой напряжения могут содержаться постоянные составляющие и субгармоники. Формулы для определения выходных частот X, при которых возможно появление постоянных составляющих и субгармоник, приведены в табл. 3. Они найдены из следующих условий: со + ± (3bs - 1)0 = Оисо± (3bs - 1) Q < со + Q.

Сравнивая все режимы работы НПЧ с ОМ, можно сделать вывод о том, что режим прямого чередования фаз при Q > со является основным, наиболее приемлемым, так кек обеспечивается высокое качество выходной энергии. В этом режиме в выходном напряжении НПЧ с ОМ отсутствуют постоянные составляющие и субгармоники во всем диапазоне изменения выходных частот.

В соответствии с соотношением (И) находим ток на выходе НПЧ с ОМ при активно-индуктивной нагрузке

/ (/со;Овь,х/ = 2Г (d) и (/со; Овьж/ =

= /msBb,xz ехр / [со ± (3&S - 1) Q] t, (35)

S=oo

Лиевых/ - ftnsBbK ехр /

(3&s-l)(/-l)--(p„

(36)

J msBbix . (37)

(p„s = arctg [CO ± {3bs -1)0] LJr„ =

= arctg {[1 -f 3&S (1 - X)/X]}; (38)

2„ = ]/r2-f (co + Qf L; (Ph= arctg [(CO+ Q)L„/r„]. (39)

Коэффициент гармоник тока нагрузки

sin а

X / sin (bsn - I) a 1

/S=-t-co Zj(6sn-1)2 „ /;\ i-tYTZ

Графики зависимости этого коэффициента от относитель-дой выходной частоты X и cos ф, рассчитанные по формуле /4О) для двухтактных и однотактиых схем, показаны на рис. 46. С уменьшением cos ф„ их коэффициент гармоник резко уменьшается. Это объясняется увеличением относитель-дой частоты V высших гармоник. Для сравнения на рис. 46 показаны графики зависимости ki = / (X) для НПЧ с двукратной модуляцией. Уменьшение ki для этих преобразователей наблюдается только при уменьшении cos ф„, и от X он не зависит.

Действующее значение тока нагрузки можно выразить

Рис. 46. Графики зависимости коэффициента гармоник тока нагрузки от относительной частоты при разных cos Фн для схем:

1, 2, 3 - однотактной; б, 8, 9 ~ двухтактной; 4, 5, 7 - ПЧ с двукратной модуляцией (/, 4, 6 - cos <р„ = 0,9;

2, S, S - cos = 0,8; 3, 7,, 9 - cos фц = 0,6)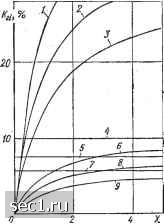

через коэффициент гармоник /вых = 36 sin а Kl -f k%/n или через действующее значение входного тока /вых = 1вхУп/т, где п, т - число соответственно входных и выходных фаз.

Токи на входе преобразователя определим с помощью соотношения (12). Для этого используем выражение (35). При числе фаз /п = 3 на выходе НПЧ с ОМ получим

I (/со; Овхб = Yi fe (О J Овых/. Подставив в это соот-

ношение выражения (25) и (35) - (39), определим ... ЗЬЮ„

1 (/со, 1)вхк =

3 +00 +ОС

sin (ba -

1) а sin (3fcs - 1) а

/=1 s=-оо а=-со

(Ьа- 1) (36s- 1) X X Vcos (рй + [1 -f 36s (1 - Х)Д]= sin= q>„ X exp / [{со + [(&a - 1) ± (3&S - 1)] fi} /-f + [=F (&a - 1) (Л - 0 + (3bs - 1) (/ - 1)] 2я/3 - фнЛ.

(41) 69

Рассмотрим аргумент полученного выражения. Коэф, фициент [фо - 1) ± (3&s - 1)] при q для любых значений S представляет бесконечную последовательность чисел

[фо - 1) ± (3bs -l)] = ±bn, (42)

где и = - оо, .... О.....+ оо.

Отсюда следует, что

фа - 1) = HF (3&S - &х - 1). (43)

Коэффициент при 2я/3 в выражении (41)

=F (Ьо - 1) (А; -/) + (ЗЙ5 - 1) (/- 1) =

= ± [фо - 1) + (3&S - 1)] (/ - 1) Т фо -1){к- 1) (44)

Использовав выражения (42) - (44), выражение (41) перепишем в виде

/(/со:Овх. = х

V у V V sin (3bs - fcx - 1) g sin (3fes -~ 1) g (36s -6x -l)(3bs-1)X

X у coss (p„ + 11 -j- 3bs (1 - X)/Xia sin (Рн

X ехр / [(со ± bxQ) / 4- &x (/ - 1) 2я/3 -

- фх+1){к-1) 2я/3 - (Phs].

При суммировании по / в этом выражении все составляющие с и, некратными 3, взаимно компенсируются. Поэтому после суммирования можно записать

/(/со; tUk= 5° 4xBxfeexp/(co±3bxQ)/, (45)

/niKBHXft = /тквх ехр / [- (Ьх -- 1) (ft - 1) 2я/3 - (ри]",

/тквх = (ЗЬ)/лГ+Ж/(яг„); (46)

= arctg (Вн/Л); (47)

д sin (3bs - fcx - 1) g sin (3bs - I) a cos ф,, .

~ 2d (3bs - bx - 1) (3bs - 1) {cos2 (p„ -f -f [1 -f 3bs (1 ~ X)/X]2 sin2 фн)

Bk =

V sin (3&S - fcx - 1) g sin (3&s - 1) a {1 -f 2bs (1 - X)/X1 sin фн ~ 2i {3bs - bK- 1) (36s - 1) {cosa (p„ 4. [1 -f 3us (1 - X)/XJ2 sin фи "