0.2 1-0.2

= 0.25 Эрл.

Р, =

ХС0.25

Р. =

с; 0.25-

Хс;о.25

= 0, = (1 - -)Ру = 0.

ЗАДАЧА 2. Емкость пучка V=%, число источников нагрузки Af=30, поступающая на вход удельная нагрузка а = 0.1; 0.3; 0.5 Эрланг. Сравнить потери по цремени, вызовам и нагрузке для моделей Эрланга н Энгсета. Решение. Модель Эрланга:

A=Na;

А=3 А=9 А=15

0.0081 0.2892 0.5193

0.0081 0.2892 0.5193

Ру 0.0081 0.2892 0.5193

2.9757 6.3972 7.2105

Модель Энгсета:

Х Сз„(а /1 - а)

С.Лд /1 - а) X С Ла /1 - а)

= (1 - 8 / 30)Р,, Г, = /4(1-Р).

а=0.1 0.0058

а=0.3 0.3479

а=-0.5 0.6761

0.0047 0.3286 0.6629

Ру 0.0043 0.2551 0.4958

Г, 2.9871 6.7041 7.5630

4.7. Полнодоступный пучок в ситеме с ожиданием Система M/M/V.

4.7.1. Стационарные вероятности

Модель справедлива при предположениях:

- вызовы, поступающие на вход системы, образуют пуассоновский поток постоянной интенсивности с параметром Я,;

- длительность занятия подчиняется экспоненциальному распределению с параметром ц;

- любой из V выходов пучка доступен, когда он свободен, для любого поступающего вызова;

- вызов, не принятый к обслуживанию в момент поступления, поступает в очередь и обслуживается в порядке постзпления;

- исходной для расчета является поступающая нагрузка;

- система находится в стационарном режиме.

Диаграмма переходов марковского процесса системы обслуживания с ожиданием изображена на рис.91.

ЗАДАЧА 1. Определить потери по времени, вызовам и нагрузке для N=5, V=%. Удельная нагрузка а = 0.2 Эрл. Решение.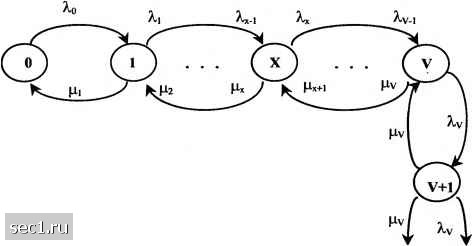

Рис.91. Диаграмма переходов системы с ожиданием Используя уравнения процесса размножения и гибели при A<Vимеем

[х] =

(Л 1цГ

x=0,l,...F,

{Я Ifi)

[0], jc=F+l,F+2,...

или, принимая А=Х/}х,

[х] =

[0],

x=0,l,...F,

JC =F+l,F+2,.

где [0] определяется из нормирующего условия

1=0 • * • x=V+\

V 00 < J[~

A<V "

У ill

0 xl VIV - A

Потери no времени равны вероятности того, что все линии заняты, она же вероятность ожидания начала обслуживания

Р,=д>0)=м4[0]=- (4.7.1) - вторая формула Эрланга.

Еу{А)

\--(1-ЕМ))

(4.7.1)

Сравним систему с потерями и систему с ожиданием. Еу{А)<

Еу(А)

Вывод: Вероятность потерь в системе немедленного обслуживания (без ожидания) меньше, чем вероятность ожидания начала обслуживания в системе с ожиданием. В этом смысле пропускная способность системы с явными потерями больше системы с условными потерями. Это объясняется тем, что 1) в системе с ожиданием доля времени, в течении которого обслуживаются вызовы меньше, 2) имеется ограничение входящей нагрузки A<V.

В системе M/M/V/N/ используются те же уравнения процесса рождения и гибели, но суммирование «ожидающих» вероятностей производится не до °о , а до Л. В результате, принимая обозначение a=A/V, имеем

Р (>о)= (-Х-")

• 1/Еу(А) + а(1-а)(1-аУ

Вероятность Рц, (>0) принимает промежуточное значение между Ev(A) и вероятностью Р(>0).

4.7.2. Система М/М/ V. Функция распределения

Обозначим через P(>t) вероятность ожидания начала обслуживания больше, чем t, а через Pt(>t) - условную вероятность ожидания начала обслуживания при поступлении вызова в момент, когда в системе находятся А: вызовов, из них Г вызовов обслуживаются, а (к-V) вызовов ожидают обслуживания. По формуле полной вероятности

р(>о=;[щ(>о.

Вероятность Pk(>t) есть вероятность того, что за время t произойдет не более 1.2,...(k-V) освобождений и вычисляется с использованием распределения Пуассона

,=0 i!

Поэтому

k=V i=0 I-

-Vf4t

k=V i=0 I-

Функция распределения времени ожидания (ФРВО) начала обслуживания или вероятность F„(t) того, что время ожидания начала обслуживания не превысит t

Fit) = l-Pi>t)l-Pi>0)e-->, (4.7.2)

а ФРВО самого обслуживания