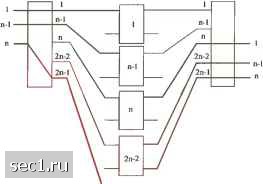
Рис.97. Неблокирующая схема Клоза

Итерационное построение неблокирующих многозвенных КП состоит в использовании процедуры замены коммутаторов одного из звеньев с ri>24 трехзвенной неблокирующей схемой Клоза. В результате получаются 5, 7, 9,... (л-У-звенные неблокирующие КП.

ЗАДЛНА I. Построить 2-звенное КП с параметрами N=128, М=Ь4 из коммутаторов емкостью Кх8. Опрвл ю кон-мутаторов. Решение.

16 коммутаторов емкостью 16x8 в первом эвене н 8 коммутаторов емкостью 8x8 - во втором.

ЗАДАЧА 2. Определить mi

f между коммутаторами в 2-Э1 коммутации О.

мКПс

Решение.

СвязностьJ, - J. mj = Пг =/, • *j= 3*3 = 9 Q=n, т, к, + пгт2 = З + ЗИЧ - 162 При построении КП в виде одноивсннон схемы (=Л/ ftj А

ЗАДАНА 3. Построить oi Решение.

Число точек коммуташ1н

iKoe по числу точек коммутаи

кп д,-64ОО0О.

эвснного КП. п,ту20. т, пкг 2п,-J 39. П2 = к, =kf=N/n, =40.

Qi = 124800 точек коммутации. Во втором звене коммутации образовались юммутагоры емкостью 40x40, которые следует заменить трехзвенлой схемоК П(щствновп(н в (4.9.1) значений NnjuMmj, получим параметры трехзвенного КП емкостью 40x40- п.А!. выбираем г, - 4. Тогда n, = mj = 4. т, = kj = 2п,-1 = 7. = bij - ft, - = 40/4 - 10.

Для 5-звашо1т, КП.-n, - nij - 20. m, - nj - JP. ft/- ft, - 40, -m-4. mnj-7. ftj=A = J«).«j = mj-/n, ft,-2?3, 0, - III540.

Окончательно:

g,-64o ooo> gj-=i24 boo > д-т 540.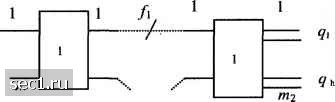

Рис.98. Двухзвенное КП

Исходные предположения:

- на вход КП поступает пуассоновская нагрузка первого рода;

- структурные параметры 2-звенного КП заданы;

- вызов, не принятый к обслуживанию в момент поступления, теряется;

- исходными для расчета являются нагрузки Aj, обслуженные каждым направлением. Примем обозначения:

а, = ZAij/ki т, - нагрузка, обслуженная одной ПЛ;

= A2J / q, - нагрузка, обслуженная в направлении одним выходом коммутатора второго звена;

Ь = а/* - вероятность занятия пучка ПЛ;

с = fltjy - вероятность занятия всех выходов одного коммутатора ву-м направлении; г = nii/fi = кг - ЧИСЛО пучков пл.

Пусть Wi - вероятность занятия / пучков ПЛ, принадлежащих одному коммутатору, а Н r-i - вероятность занятия выходов в направлении у (r-i) коммутаторов 2-го звена, к которым ведут свободные ПЛ. Тогда вероятность потерь в у-м направлении

(4.\Q.\)

(4.\Q.\) - комбинаторная формула Якобеуса (C.A.Jacobaeus).

При отсутствии сжатия и расширения справедливы равенства: п, = т, ,

П2 > qi

ZA2, = т, к, а,.

Для описания вероятности занятия группы ПЛ примем распределение Бернулли

4.10. Расчет потерь в двухзвенных коммутационных полях

По сравнению с однозвенными полнодоступными схемами и однозвенными НС, звеньевые схемы имеют очень большое число состояний. Поэтому во многих практических случаях система уравнений не может быть даже составлена. Единственный выход - применять приближенные методы расчета. В режиме линейного искания 2-звенные схемы не экономичны, поэтому они практически используются только в режимах группового и свободного искания. Для расчета потерь в двухзвенных КП наиболее известен комбинаторный метод Якобеуса.

Структурная схема двухзвенного КП приведена на рис.98.

4.11. Расчет потерь в многозвенных коммутационных полях 4.11.1. Метод вероятностных графов. Модель Ли (С. Y.Lee)

Исходные предположения:

- на вход КП поступает пуассоновская нагрузка первого рода;

- структурные параметры многозвенного КП - s, kg, щ, irig.fg, h, q,, известны;

- вызов, не принятый к обслзиванию в момент поступления, теряется;

- исходными для расчета являются нагрузки А,,, обслуженные каждым направлением. В соответствии с режимом искания составляется граф путей, в котором каждая из Vg

ветвей, состоящая из ПЛ, занята с вероятностью bg =agH свободна с вероятностью (1- bg), причем ag = Asyjkgnig, as, = Asj/qjks, Vg = mfg, А,ут = 2И,-.

Потери вычисляются как вероятность отсутствия свободных соединительных путей к требуемому выходу (или выходам). Расчет производится рекуррентно от *-го звена к первому.

w,c\b\\-by-\ Я, ,=с-,

Поступающая нагрузка нау-ое направление находится из равенства

При наличии сжатия справедливы равенства: п, > т, , Пг > , = к, т, а,.

Дополнительные потери возникают при занятости всех выходов коммутатора 1-го звена:

Pj =Ь+ф + с-ЬсУ\г,=1 =а," +а,/ -а,а,/Г-При наличии расширения справедливы равенства: л/< т/, П2> qj, EAj = к,т,а,. Pj =(Ь + с-ЬсУ\г,.г =(а, +а,;

ЗАДАЧА 1. Определить потери и поступающую нагрузку в КП с параметрами: п, = т, = к, = пз = гпг = кз = 8, h = 4, q, = Я2 = дз-д4 = 2, A21 = А22 = А23 =А24= П .2 Эрл. Решение.

а2, = А2,/к2Ч2 = а22 = 023 = 024 = 0.7, а, = 0.7.

Я, = (а, + Сз," - а.сг,")" = (0.7 + 0.7 - 0.7 * 0.7) = 0.85 = 0.272 ,

ЗАДАЧА 2. Определить потери и поступающую нагрузку в КП с параметрами: И/ = 16. гп/ = к, = П2 = т2 = к2 = 8, h = 4, qi =42 =Чз=Ч4 =2.A2i =22 Агз =А24 = 11.2 Эрл. Решение.

021 = A2ifk2q2 = 022 = 023 = о24 = 0.7, о, = 0.7.

Я, = а," + (а, + 02," - a.fli/)" = 0.7* + 0.272 = 0.329 ,

0, - = ---= 16 . 707 Эрл.