Рис.101. Объединение и просеивание потоков в сети

4.16.2. Оценка суммарного потока

Ранее были рассмотрены характеристики двух просеянных потоков: в 4.5.2 - потока Эрланга и в 4.5.3 - потока Haj ьма. На рис 102 для примера показаны: а) порождающий поток вызовов, б) просеянный поток Эрланга 4-го порядка и в) просеянный поток Пальма 4-го порядка.

Как видно из рисунка при одинаковой интенсивности просеянных потоков на интервале среднего врамени занятия ts характер потоков существенно разнится, хотя они и создают одинаговую нагрузку. Просеянный поток Эрланга Jt-ro порядка описывается достаточно простым выражением

(Xt)

I(k,Xt)

где /(АД /) = J(>. / +z)*e rfz - интеграл первого рода, X = А/(к+1) - параметр

просеянногопотока. Л параметр порождающего гютока вызовов.

Просеянны поток Пальма считается только численными методами и не имеет явного аналитического выражения, хотя его параметр после просеивания полнодоступной схемой известен - ЛЕ/Л). Поэтому для аналитического описания типа суммарного потока вызовов приходится прсдазводить подмену потока Пальма потоком Эрланга той же интенсивности.

параметром Л (на рис. 101 - жирная красная линия) и поток от части абонентов станции А с параметром "к. При расчете характеристик системы коммутации в предыдущих разделах было необходимо знать тип и параметры поступающего потока вызовов. Если поток собственных вызовов станции С можно вполне считать простейшим араметром Л , то тип потока с параметром Xj, можно определить только зная процедуру провеивания потока станцией А. Тогда встают вопросы: как классифицировать суммарный поток вызовов с параметром (Л+ Х)? В частности, в каких случаях суммарный поток вызовов можно считать простейшим и пользоваться соответствующими формулами ?

1 1 I I I III II I I I II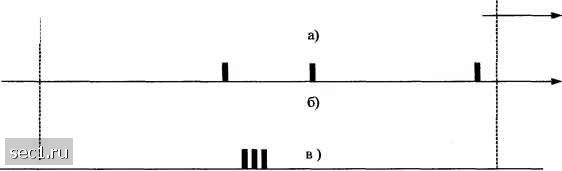

Рис.102. Просеянные потоки а) порождающий поток вызовов, б) просеянный поток Эрланга 4-го порядка, в) просеянный поток Пальма

Процедура классификации суммарного и-мерного потока вызовов сводится к следующему.

1. Определяется эквивалентное значение параметра порождающего потока вызовов

1.=".-

2. Определяется суммарный параметр просеянного потока вызовов

3. Вычисляется коэффициент просеивания суммарного потока вызовов

А:= KJX S - 1.

4. Рекомендуются функции распределения (ФРВО)

F(0 = l-exp(-X,0, к<\.

F{t)

ехр(-ЛД к>\.

ЗАДАЧА 1. Показать, что суммарный поток, полученный объединением простейших потоков - простейший. Решение.

В этом случае Л j - А, ; . п

А, =

Ел,-

V ,=1 J

f.=Ч-. 1,= Х.. * = Л./Я,-1.

При П 00 параметр возрастает гораздо медленнее, чем Я, j, что приводит к постепенному снижению значения

к = i I х j-l,a это и означает, что по своим свойствам суммарный поток вызовов все более будет приближаться к простейшему.

В частности, при объединении п одинаково просеянных потоков с параметром Л каждый, среднее значение параметра порождающего потока остается постоянным = Л, а суммарный параметр просеянного потока Я,, = п Я,,.

ЗАДАЧА 3. Классифицировать суммарный поток, полученный обьехшнением простейшего потока с параметром Aj = 100 час" и потока с параметром Л2 = 200 час", потерянном на 100-линейном пучке. Решение.

Ai= 100, 100, kl = О,

Л2=200, 2 = 200100(200) =100, h = 1,

Л, = 150, К = 200, А: < 0.

Суммарный поток - тфостейшийс ФРВО

F(t) = 1 - ехр (-2001).

ЗАДАЧА 4. Классифицировать суммарный поток, полученный объединением простейшего потока с параметром Aj - 100 часи потока с параметром Л2 - 200 час, потерянном на 220-лииейном пучке. Решение.

Л,= 100, 1 = 100, kl = О,

Л2=200, Я2=200£ио(200)=2.2, h= ю,

Л, = 102.1, Xs = 102.2, k<q.

Суммарный поток - простейший с ФРВО

F(t) = 1 - ехр (-102.21).

ЗАДАЧА 5. Классифицировать суммарный поток, полученный объединением потока с параметром Aj = юо час " ,

потерянном на 84-линейном пучке и потока с параметром Л2 = 200 час, потерянном на 153-линейном пучке. Решение.

Al = 100 \ = 100£в4(100) =20, kl = 4,

Л2 = 200, 2 = 200£,5з(200) =50, кг = 3,

Л, = 171.4, Кж к=\а5.

Суммарный поток - поток Эрланга 1.45-порядка с ФРВО

1 . 45 . 171 4 )

F (О = 1 - --«"РС - 171 .4 О.

/ (1 .45 , О )

ЗАДАЧА 6. Классифицировать суммарный поток, полученный объединением простейшего потока с параметром Aj = i

часи потока с параметром Aj = 200 час, потерянном на 220-линейном пучке. Решение.

Л,= 1 1, А:,= О,

Л2 = 200, 2 = 200£j2o(200) =2.2, кг = 89,

= 137.8, >s = 3.2, к = 42.

Суммарный поток - поток Эрланга 42-псфядка с ФРВО

I (42. 137.8Л

F(0 = 1--=-ехр(-137.80.

/(42, 0)

ЗАДАЧА 2. Показать, что суммарный поток, полученный объединением многих просеянных потоков, стремится к простейшему.

Решение.