
 | |
|
НПО Системы Безопасности (499)340-94-73 График работы: ПН-ПТ: 10:00-19:00 СБ-ВС: выходной  |
Главная » Периодика » Безопасность 0 ... 15161718192021 ... 101 то все зависит от того, какая цифра появляется в знаковом разряде при сдвиге: нуль при S -2. В первом случае к сдвинутому числу необходимо прибавить корректирующее число (5-1). 00... О, а во втором случае - корректирующее число. 1.00...0. Пример 1.21. Пусть в четверичной системе канонического типа с цифрами О, 1, 2, 3 требуется найти сумму чисел < X >4 = -0,2301 и <у>==- 0,2033. Переходя к обратному коду, получаем , •• И„ = 3.1032 Щ = 3.1300 . 1 2.2332 I t . • - - . , 2.2333 Появление в знаковом разряде цифры 2 вместо 3 показывает, что произошло переполнение. Для устранения переполнения сдвинем числовую часть результата на один разряд вправо с учетом потери при сдвиге крайнего ппавого разряда результата. После сдвига получии 2.2233. Теперь прибавим к сдвинутому числу корректирующее слагаемое 2.0233 • - " 2.0000 3.2233 <;c--j;>4 = 4.(-0,1100). • Полученный результат соответствует истинному значению суммы. Теперь рассмотрим переполнение для случая 5 = 3,2. Для троичной системы 5 - 2 = 1. Поэтому в такой системе переполнение может быть обнаружено, но не может быть исправлено. Для двоичной системы 5--2 = 0, а 1-5-1. Это означает, что переполнение в двоичной системе вообще не обнаруживается, так как машина не может отличить неправильный результат от правильного. В случае 5 = 2 при переполнении для машины происходит просто смена знака результирующего числа. Для возможности исправления переполнения в троичной и двоичной системах счисления приходится вводить специальный контрольный разряд, помещае- мый слева от знакового разряда. Контрольный разряд заполняется так же, как и знаковый. Коды, содержащие кроме знакового разряда еще и контрольный разряд, называотся модифицированными кодами. Поэтому можно говорить о модифйцированно! прямом, дополнительном или обратном коде. Для модифицированного кода мы будем исполь- зовать обозначения [х], [х\ или \х]. Если в результате суммирования в модифицированном коде в троичной системе в знаковом и контрольном разрядах стоят одинаковые цифры 00. или 22., то это соответствует отсутствию переполнения. При наличии переполнений для суммы двух положительных чисел в знаковом и контрольном разрядах возникнет комбинация 01., а при наличии переполнения при суммировании двух отрицательных чисел в этих разрядах возникнет комбинация 21. . Таким образом, будет обнаружено переполнение при суммировании и-результат сложения может быть исправлен. Аналогичное положение получается и.для двоичной системы. При отсутствии переполнения в знаковом и контрольном разрядах суммы стоит комбинация 00. или 11. . Если же произошло переполнение, то при суммировании положительных чисел в знаковом и контрольном разрядах будет стоять комбинация 01., а при суммировании отрицательных чисел - комбинация 10. . Таким образом, с помощью модифицированных кодов можно обнаружить и исправить ошибку переполнения при суммировании в троичной и двоичной системах счисления. Пример 1.22. Пусть требуется сложить в двоичной системе счисления числа- < х >2 == 0,101101 и >2 = 0,011100. Переходя к дополнительному коду, получаем = 0.101101 • = 0.011100 * ~ 1.001001, и ошибка переполнения не обнаруживается. При не-модифицированном коде машина прочитает результат сложения, как < х-b v>2 = -0,110111, что совершенно не соответствует .настоящему результату. Перейдем теперь к модифицированному дополнительному коду , Нмд = оо.101101 • . М„,=,ооотоо :* " 01.001001. Появление- в знаковом и контрольном разрядах комбинации 01. указывает на переполнение. Для устранения переполнения необходимо . произвести сдвиг результата вправо на один разряд. После сдвига получим число 00.100100. Прибавление коррек-тиру-ющего слагаемого в случае двоичной системы не требуется, если при сдвиге числа содержимое контрольного разряда числа после сдвига совпадает с тем значением, которое было записано в нем до сдвига. Так как модифицированный код необходим только для контроля при сложении, то нет необходимости хранить информацию в памяти машин в модифицированном коде, так как это привело бы к большому и малоэффективному расходу оборудования для записи содержимого контрольногоразряда. Поэтому практически контрольный разряд формируется лишь при передаче числа в сумматор путем размножения Содержимого знакового разряда поступающего в сумматор числа. До сих пор мы предполагали, что суммирование чисел происходит на сумматоре параллельного типа, показанном на рис. 1.3. Однако все наши выводы верны и для случая суммирования чисел с помощью сумматора последовательного типа, схема которого изображена на рис. 1.5. В этом сумматоре имеется всего одна одноразрядная суммирующая схема, на вход которой подаются суммируемые числа, начиная с младших разрядов. Перенос в стар- 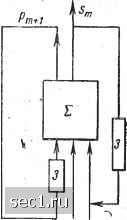 Рис. 1.5 0 ... 15161718192021 ... 101 |