
 | |
|
НПО Системы Безопасности (499)340-94-73 График работы: ПН-ПТ: 10:00-19:00 СБ-ВС: выходной  |
Главная » Периодика » Безопасность 0 ... 21222324252627 ... 101 Разбиваем данное число на две частиц; =0,2100 и =-0,0002. Эти два числа суммируем на обычном сумматоре с помощью обратного кода, [jU = 00.2100 22.2220 . 100.2020 I-1- 00.2021 ; Окончательно, (л:)з = 0,2021, Пример 1.33. Найти сумму чисел (л:),о = 0,76486 и (j)io =- 0,39471 в квазиканонической системе счисления. Используя квазиканоническую систему с цифрами от -6 до 5 и правила перехода, получим {х}[о== = 1,36514 и (j;),o = 0,40531. Теперь осуществляем суммирование по правилам параллельного сложения в два этапа 1,35614 "0.4053Т • . 1 34025 промежуточная сумма О.ТПОО перенос в старший разряд 0.43025 Окончательно (л:)!о = 043025 или, переходя к каноническому представлению, (л:),о = 0,37015. Отметим, что знак числа в квазиканонической системе счисления, как и в симметричной канонической системе, определяется знаком старшей значащей цифры в записи числа. Некоторую трудность в квазиканонической системе создает проблема определения переполнения разряднбй сетки. Как видно из проделанных выше примеров, квазиканоническое представление числа, по модулю меньшего единицы, может быть числом, большим единицы (как, например, случилось при переводе десятичного числа 0,76486 в примере 1.33 в квазиканоническую десятичную систему). /Для обнаружения переполнения исследуются два старших разряда квазиканрнического представления. Этими разрядами являются нулевой разряд й разряд с весом 5"*. Если в нулевом разряде стоит число, большее единицы, или в нулевом разряде стоит единица, а в разряде с весом 5~* - положит-ельная цифра, то имеет место положительное переполнение. Если же в нулевом разряде стоит отрицательная цифра, по. модулю большая единицы, или в нулевом разряде стоит цифра минус единица, а в разряде с весом - отрицательная цифра, то имеет место отрицательное переполнение. Для оценки диапазонов переполнения укажем, что безусловное переполнение имеет место для числа х, которое удовлетворяет неравенству \х+\\>\ + ----q, л - 1.1 где q означает цифру с максимальным по абсолютному значению количественным эквивалентом. Переполнение невозможно, когда Если же число х удовлетворяет неравенству то переполнение становится возможным, но не обязательно происходит (область вероятностного переполнения). С целью уменьшения количества различных цифр в системе счисления можно перейти к модифицированным квазиканоническим системам счисления, для которых число избыточных цифр равно единице. Покажем, что переход к такому представлению чисел приводит к тому, что при суммировании возникают переносы не более чем на два разряда. На рис. 1.8 показан сумматор, работающий по принципу переноса только на два разряда влево. В этом случае s\w] + p], ; ... . Для любого 5> 2 принимает-. + 1 значение. Цри четном 5 ---<«;< у. На первом шаге перенос [;j=l вырабатывается, если \xi + y[\> - . На втором шаге , суммирования перенос Ipij. == 1 выра- когда одновременно не могут батывается только тогда. Это означает, что pl и быть равны 1 или -1, а может принимать только 5+1 значение из того же множества, что и w, S значения w лежат в ±0,5(5 + 1). Для пред- при нечетном основании пределах от ±0,5(5-1) до ставления числовой информации в памяти машины достаточно иметь возможность представления (5+1)-й цифры. Но для возможности замены операции прямого вычитания операцией сложения с дополнением необходимо в сумматоре иметь возможность представления 5+2 различных цифр. Отметим, что при модифицир ованном квазикано ническом представлении чисел за счет некоторого упрощения самого представления (число различных цифр по сравнению с квазиканонической системой меньше на единицу) повышается время произ- . Рис. 1.8 водства операции ело- . жения. Учитывая, что основное время во времени переноса для обычной Системы счисления для близких 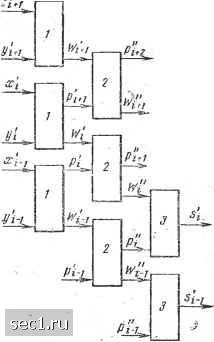 0 ... 21222324252627 ... 101 |