значениями qi,pvi q, характерными для атих задач. На рис. .3.1 показаны графики, отражающие общий вид функции V () для случая, когда в качестве решаемых на машине задач рассматривались задачи численного решения уравнений в частных производных. Как видно из этих графиков, значение А = 4, например, является оптимальным, так как для всех программ

оно дает экономию

500.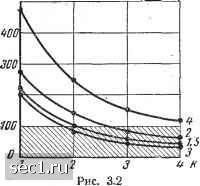

-200

,более чем в два раза. Усреднение по показанным на рис. 3.1 программам дает при = 4 экономию во времени в 2,5 раза.

На рис. З.Й для тех же пяти программ приведены кривые, показывающие влияние отдельных составляющих времени операции на общее время операции. Если при обычном двоичном представлении (=1) основное время уходит на операцию нормализации, то при А = 4 общее время операции в основном состоит из времени непосредственного суммирования. Для четырех программ из пяти,, исследовавшихся на машине, время нормализации составило лишь 50% от Ьбщего числа времени операции.

Полученная оценка является завышенной, так как мы исключили из рассмотрения необходимость нормализации результата вправо, что возможно и при переходе к представлению порядков по основанию 2 Однако это завышение не является существенным, и результаты оценки функции v (k) практически правильно отражают описываемый процесс.

Д,ля реализации описанной методики выполнения операций необходимо ввести некоторое дополнительное оборудование. Если при сдвиге вправо мы теряем разряды мантиссы, то при последующем сдвиге влево ощибка из младшего разряда мантиссы может переместиться в старшие разряды и стать весьма большой.

Для устранения этой неприятности необходимо при переходе к представлению порядков в системе счисления с основанием 2* добавить к мантиссе справа k дополнительных разрядов. Однако рост длины разрядной сетки на представление числа выражается не линейной функцией V{k) = k, а представляет собой функцию, показанную на рис. 3.3. . Объясняется это тем, что при переходе записи порядков -в системе (Счисления с основанием 2* число разрядов, отводимых для хранения порядков чисел, при сохранении диапазона представления чисел становится меньшим и высвобождающиеся разряды могут быть использованы в качестве дополнительных для записи мантиссы числа. Поясним это на примере. Пусть в двоичной системе для записи порядков использовалось пять разрядов. Если теперь порядки записываются в шестнадцатиричной сис- о 4 7 3 5 6 7 8 9 W П теме, то для сохра- Рис аз

нения того же диапазона изменения порядков 2~, 2 достаточно всего двух разрядов, ибо диапазон 16", 16 перекрывает диапазон, используемый при двоичном представлении. Освободившийся разряд порядка может быть использован для записи мантиссы. Введем оценочную функцию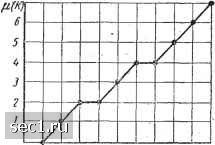

v(A).f.(ft)

показывающую, во сколько раз уменьшается время выполнения операции сложения на один разряд дополнительного оборудования. График этой функции строится на основе графиков функций v() и t(fe). Он приведен на рис. 3.4. В Качестве оптимальнЬгх значений к, как видно из этого графика, следует принять ==2,4. Из. этих значений = 4 более предпоч-

тительно, так как оно при двух дополнительных разрядах обеспечивает более существенное ускорение операции сложения.

Некоторые трудности вызывает описанное представление чисел при реализации операции деления. Так как сдвиг влево и вправо происходит сразу на k разрядов, то возможность получения целой части частного становится нежелательной. Для устранения

такой. возможности можно путем предва-рительюй проверки мантисс делимого и делителя выяснить, какая из мантисс больше. Если мантисса делимого не меньше мантиссы делителя (по абсолютной величине), то необходимо изменить мантиссу делимого с помощью сдвига ее вправо на k разрядов с соответствующим изменением порядка делимого.

Пример 3.7. Разделить число (л:)21б= 16-0,11010110 на-число (>)2,1б= 16-0,00111100.

Для осуществления деления сравниваем между .собой величины мантисс. Для этого вычитаем модуль мантиссы делителя из модуля мантиссы делимого. Вычитание заменяем счожением в модифицированном дополнительном коде

длМмд= оолююио *[-тз,]„д = 11.11000100

01ТЗЧ5ьТ83 10 11К Рис. 3.4

lOO. 10011010

Положительный результат вычитания свидетельствует о том, что мантисса делимого больше ман-. тиссы делителя. Поэтому преобразуем число х следующим образом: (л;)2,1б= le-OOOOOl 1010110. Правые четыре разряда при этом не теряются, так как для их представления имеются дополнительные разряды,