Вместо множества главных элементов можно брать любое множество М, элементы которого получаются

из элементов М прибавлением числа k Y\ Pi-

.1=1

Пример 6.3. Для системы модулей: Pj = 2, Рг = 3

и Рз = 5 множество М состоит из 30 элементов от О

до 29. Код в остатках, например, для элемента 14

14 14 14

есть rest -; rest -; rest - =0, 2,4. Вместо множества 2 3 5

М можно взять какое-либо множество М. Примером такого множества может служить множество чисел от 60 до 89.

Задачи

1. Доказать следующее утверждение: если а и & сравнимы по модулю р и d есть делитель р, то й и & сравнимы по mod d.

2. Доказать, что если одна часть сравнения и модуль имеют •общий делитель, то вторая часть сравнения делится на это же число.

3. Найти вид чисел хну, удовлетворяющих системе сравнений . .

л + у = 2 (mod 3); Зх -3j;=18(mod9).

4. Дана система модулей: = 5, g = 6 и = 11. В множество М/1 входит число 1000. Найти остальные элементы множества М-

§ 6.2. Представление чисел в коде в остатках

В настоящем параграфе мы будем считать, что задано некоторое множество модулей р., являющихся взаимно простыми числами, и в качестве множества

выбрано множество главных элементов М.

Если в качестве модулей используются простые числа, то диапазон представимых чисел (произведение модулей)характеризуется таблицей 6.2.

Второй и третий столбики в этой таблице показывают, сколько двоичных разрядов необходимо использовать в вычислительной машине на разряд кода в остатках, соответствующий данному модулю, и суммарный расход двоичных разрядов на представление всех чисел из диапазона, определяемого произведением модулей.

Таблица 6.2

Одной из проблем, связанных с представлением чисел в коде в остатках, является проблема представления отрицательных чисел. Подобно смещенным системам счисления код в остатках представляет множество чисел только одного знака (положительных или отрицательных). Для представления отрицательных чисел необходимо ввести некоторый аналог допол-Нительного кода,1 ис-лользовавшегося в канонических системах счисления.

На рис. 6.1 схематично показано множество чисел М для некоторой совокупности модулей. Для представления отрицательных чисел необходимо разбить это множество на два непересекающихся подмножества

М и М" и считать, что коды из М используются для кодирования положительных чисел, а коды из-М" - для кодирования отрицательных чисел. При этом желательно, чтобы М и М" были бы по возможности равномощными (т. е. желательно приблизить код в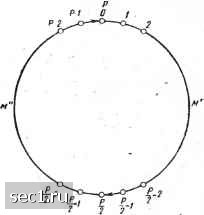

Рис. 6.1

остатках к обычному представлению в смещенных системах счисления). Чаще всего разбиение М на М и ЛГ производят так, как показано на рис. 6.1. При этом интервал чисел от О до 0,5р (не включая правый конец интервала) отводится для положительных чисел, а интервал от 0,5р до р (не включая правый конец интервала) - для отрицательных чисел. Здесь \М"-\ = ==Ж и р предполагается четным*.

В этом случае вместо отрицательного числа х рассматривается его положительное дополнение до р, т. е. [-л;]д =р -\х\.

Пример 6.4. Найти диапазоны представления чисел, если система модулей имеет вид р, =2, р2 = 5, Рз=7.

В этом случае р = 70, и, следовательно, множество М Состоит из 70 элементов. При необходимости представления в машине как положительных, так и отрицательных чисел этот диапазон становится равным <-Ь34, -35). Как мы видим, этот диапазон является несимметричным.

Пример 6.5. В системе модулей предыдущего примера найти код в остатках для чисел (л:),о = 30 и 0)10=-17.

Для числа 30 код в остатках получается нахождением остатков от деления на модули системы (л:) = = 002. Для числа -17 необходимо перейти к дополнительному коду. Тогда мы получим число 53. Таким образом, (у) = 134.

Остановимся теперь на проблеме перевода кода в остатках некоторого числа из Ж в обычное каноническое представление в десятичной системе. Метод, который мы рассмотрели для решения подобной задачи в предыдущем параграфе, не может считаться приемлемым, так как этот метод сводится к полному перебору всех (или почти всех) возможных - вариантов и требует большого машинного времени.

Для решения поставленной задачи мы рассмотрим переход от кода в остатках в полиадическую систему, тесно связанную с кодом в остатках для данной системы модулей Pg,...,/?„, p„+i}. В этой системе вес i-ro разряда равен Qi = qi-iPi. Вес нулевого разряда равен единице. Для системы, состоящей из п

* I Af I означает число элементов М.