кость должна находиться в силовом поле, имеющем потенциал. Но если gidhi = g2dh2, то для соблюдения равновесия требуется, чтобы соблюдалось также равенство pi = Р2- Следовательно, неоднородная жидкость может находиться в устойчивом равновесии только в силовом поле, имеющем потенциал. Поверхности равного потенциала являются одновременно поверхностями равного давления и равной плотности.

Таким образом, равенства (16) и (17) применимы и к неоднородной жидкости. Условия равновесия остаются такими же, какими они были выведены в § 6 и 7 для однородного поля тяжести.

Почти все силовые поля, встречающиеся в физике, за исключением магнитных полей, вызванных электрическим током, имеют потенциал, поэтому приведенное выше условие о существовании потенциала практически не вносит никакого ограничения. Но другое условие - постоянство плотности на каждой поверхности равного потенциала - практически весьма важно. Оно может но соблюдаться, например, в том случае, когда жидкость или газ в каком-нибудь месте нагревается. Это приводит к уменьшению плотности в этом месте, вследствие чего равновесие становится невозможным, так как нагретая жидкость приходит в движение и увлекает за собой соседние части жидкости. Только после того, как наиболее нагретые части жидкости расположатся выше других частей, устанавливается состояние покоя.

Свободная поверхность жидкости или поверхность раздела двух между собой несмешива-ющихся жидкостей разной плотности всегда совпадает с поверхностью равного потенциала. Поэтому поверхности равного потенциала называются также поверхностями уровня. В геодезии поверхность моря является основной поверхностью уровня; относительно этой поверхности производится отсчет всех высот.

Поясним применение установленных выше законов на простом примере. Рассмотрим равновесие весомой однородной жидкости, покоящейся относительно сосуда, равномерно вращающегося вокруг вертикальной оси (рис. 19). Прежде всего найдем потенциал силового поля. Он, очевидно, складывается из двух потенциалов: потенциала поля тяжести и потенциала поля центробежной силы.

Рис. 19. Жидкость во вращающемся сосуде

С/2 = - / a;Vdr = -

Следовательно, полный потенциал равен

и = U+U2=UQ+gz = (18)

Поверхности равного потенциала мы получим, полагая и U = const:

Z = const -I---.

Таким образом, свободная поверхность и все поверхности равного давления представляют собой параболоиды вращения с общим параметром Дг.

Интегрируя соотношение

dp = -pdU,

мы найдем давление р в любой точке жидкости как функцию потенциала U:

р-ро = -pU, (19)

где ро есть давление на свободной поверхности С/ = 0. Подставляя в равенство (19) вместо и его выражение из равенства (18) и заменяя pg через 7, мы получим:

2 2

р = const -Ь7(-г + )-

Возьмем цилиндрические координаты г, z, причем ось z направим вертикально вверх. Тогда потенциал поля тяжести будет равен

Ui=Uo+ gz,

где g есть ускорение свободного падения, а С/о - произвольное начальное значение потенциала. Потенциал поля центробежной силы определяется ускорением шг где w есть угловая скорость вращения, общая для сосуда и жидкости. Подставляя это значение ускорения в соотношение (15) и интегрируя в направлении ускорения, т.е. в направлении г, мы найдем потенциал поля центробежной силы:

§ 11. Поверхностное натяжение (капиллярность). Как показывают наблюдения, свободная поверхность жидкости стремится уменьшить свою площадь. Это свойство объясняется тем, что свободная поверхность находится в напряженном состоянии, подобном тому, в котором находится равномерно натянутая тонкая пленка. Причиной такого состояния является следующее: каждая частица жидкости, находящаяся вблизи свободной поверхности, притягивается соседними частицами; результирующая всех этих сил притяжения направлена внутрь жидкости, вследствие чего на поверхности остается ровно столько частиц, сколько безусловно необходимо для образования свободной поверхности. Такое же явление наблюдается и на поверхности соприкосновения двух несмешивающихся между собой жидкостей. Указанное выше напряженное состояние называется поверхностным натяжением,

а иногда - капиллярным натяжением. Последнее название обусловлено тем, что поверхностное натяжение особенно резко наблюдается в тонких, так называемых волосных или капиллярных трубках.

На плоских поверхностях соприкосновения поверхностное натяжение не наблюдается, так как на таких поверхностях все силы натяжения сами по себе образуют уравновешенную систему сил. Но на искривленной поверхности силы натяжения сами по себе не могут уравновешиваться, следовательно, должна существовать какая-то сила, которая, уравновешивая силы натяжения, обеспечивает равновесие. Такой силой является разность давлений pi - р2, по обе стороны от поверхности соприкосновения. Вырежем на поверхности соприкосновения небольшой криволинейный прямоугольник со сторо-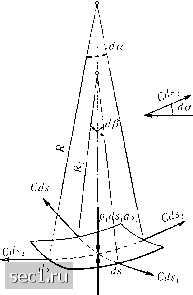

p,dsids..

Рис. 20. Равновесие элементарной площадки на поверхности соприкосновения двух весомых жидкостей

нами dsi и ds2 (рис. 20). Тогда вследствие разности давлений pi - р2 на площадь прямоугольника будет действовать сила (pi - p2)dsids2. Поверхностное натяжение приводит к тому, что на каждую сторону