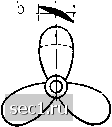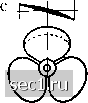Рис. 178. а) воздушный винт; Ь) тихоходный водяной винт; с) быстроходный водяной винт

что при приближении абсолютного давления в воде к нулю в последней начинается выделение пузырьков воздуха и образование пара. Это явление называется кавитацией (см. §2 гл. V). Для предупреждения слишком сильного понижения давления на подсасывающей стороне быстро вращающегося профиля толщина последнего, а также его угол атаки должны быть очень небольшими, поэтому лопасти быстро вращающихся водяных винтов делаются очень широкими. На рис. 178 показаны воздушный винт (а), тихоходный водяной винт (Ь) и быстроходный водяной винт (с) для быстроходного теплохода. Профили воздушных винтов, окружные скорости которых приближаются к скорости звука, также выполняются очень тонкими, но обычно с очень узкими лопастями (вследствие высокого динамического давления).

Имеются также винты, окружная скорость которых превышает скорость звука; однако при работе такие винты, вследствие появления изображенных на рис. 252 (см. стр. 401) звуковых волн, издают очень громкий звук, похожий на звук тромбона и распространяющийся особенно сильно в направлении, перпендикулярном к направлению полета.

На основе представлений теории крыла можно развить более точную теорию гребного винта, хорошо отражающую действительные соотношения. Эта теория, начало которой положено в работе Бетца, в настоящее вре-

BetzA., Schraubenpropeller mit geringstem Energieverlust с добавлением Л. Прандтля. Gott. Nachr. 1919, стр. 193 (помещено также в Vier Abhandlungen zur Hydrodynamik und Aerodynamik, стр. 68).

мя широко применяется для расчета воздушных винтов. Более строгое вычисление распределения циркуляции вдоль радиуса лопасти было выполнено

С. Гольдштейном. На рис. 179 показано распределение циркуляции для многолопастного винта; изображенная кривая дает представление также о распределении тяги на единицу площади сметаемого винтом круга в различных его зонах. Распределение тяги вдоль отдельных лопастей получается отсюда умно-Рис. 179. Распределение циркуля- доением на где .г есть число лопас-

ции вдоль радиуса лопасти Вычисление распределения цирку-

ляции получается особенно простым для случая узких лопастей и малой относительной поступи.

Действительные свойства водяных и воздушных гребных винтов устанавливаются путем опыта. Здесь мы остановимся только на таких опытах, при которых винт исследуется в изолированном состоянии в невозмущенной жидкости, а не в сочетании с самолетом или кораблем. При испытании вместе с самолетом (или кораблем) последний вносит значительные возмущения в движение жидкости, кроме того, винт и самолет определенным образом взаимодействуют друг с другом, что в конечном итоге делает общую картину движения очень сложной. Наиболее удобной величиной, к которой следует относить все результаты опытов, является, очевидно, отношение скорости продвижения винта ?;= Л к его окружной скорости и, т.е. величина

- = - = А и ruj

называемая относительной поступью (г есть радиус винта, aw - угловая скорость вращения). Для гребного винта, лопасти которого имеют постоянный шаг h, существует такая относительная поступь Ai, при которой винт движется в жидкости, испытывая только сопротивление трения. Как легко видеть,

Ai =

Только для значений А < Ai лопасти винта имеют относительно направления потока угол атаки, создающий положительную силу тяги.

iQcldstein S., Proc. Роу. Soc. London (А), т. 123 (1929), стр. 440. Walchner О., Luftf.-Forsch., т. 13 (1936), стр. 103. ЗСм., например, Betz А., ZAMM, т. 7 (1927), стр. 431.

Для значений Л > Ai винт начинает работать как ветряк (см. ниже, п. Ь). Для практически выполняемых винтов, у которых шаг лопасти вдоль радиуса переменный, имеют место аналогичные соотношения, только отпадает простая геометрическая интерпретация величины Ai.

Величинами, которые измеряются при опытах, являются тяга винта 5 и вращающий момент мотора D, необходимый для вращения винта. Потребная мощность равна

L = Вш,

а полезной мощностью по-прежнему будет

Lo = Sv,

следовательно, коэффициент полезного действия равен

, = (128)

Для представления результатов опыта в форме, не зависящей от размеров исследуемого винта, применяются безразмерные величины, составляемые таким же образом, как аналогичные величины в теории крыла. В Германии наиболее употребительными являются следующие величины:

ks = -= -, (129)

kd = = = . • (130)

рижг ршжг ршжг

в том случае, когда тяга и вращающий момент относятся к динамическому давлению, вычисленному не для скорости и, а для скорости v, вводятся аналогичным образом составленные коэффициенты Cs и Cd-Так как v = Xrcj, то при использовании коэффициентов kg и kd равенство (128) принимает вид:

V=. (131)

На рис. 180 построены кривые, изображающие зависимость kg, kd и Г] от X для воздушного винта, показанного на рис. 178, а. Мы видим, что кривые kg и kd вблизи значения А = 0,35 пересекают ось А,