Рис. 213. Волна уплотнения

Рис. 214. Волна разрежения

не уплотнение, движутся частичные уплотнения с тем большей скоростью, чем на большую величину уже повысилось давление; следовательно, голова волны движется быстрее ее основания и с течением времени догоняет его (рис. 213). В тот момент времени, когда голова волны догоняет основание, возникает прерывное изменение давления, так называемый скачок уплотнения, о котором подробно будет сказано ниже. В случае волны разрежения основание волны отстает от ее головы, вследствие чего форма волны делается постепенно все более и более пологой (рис. 214).

§ 3. Одномерный установившийся поток газа со значительными изменениями объема. Будем рассматривать поток газа как одномерный. В таком случае вдоль линии тока соблюдается обобщенное уравнение Бернулли [см. § 4 гл. II, уравнение (11)]. Если пренебречь силой тяжести, а также, как мы всегда будем делать в этой главе, трением, то обобщенное уравнение Бернулли примет вид:

= const = Pi,

где Р есть функция давления, равная

или, если свести удельный объем =

Р = J vdp.

Если удельный объем v известен как функция давления, то величину Р можно вычислить как площадь, ограниченную кривой v = р>{р).

Подставив это значение р в интеграл (8) и выполнив вычисления, мы получим:

Если Pl есть давление, при котором скорость движения газа w равна нулю, следовательно, в случае истечения газа из напорной камеры - давление в камере, то из уравнения (7), после подстановки в него значений Р и Pl, мы получим:

>f-l-,

(10)

Легко видеть, что скорость движения, приобретаемая газом при расширении до самого крайнего вакуума, имеет конечное значение. Этой скорости в уравнении (10) соответствует давление р = О, следовательно, она равна

2я Pl /„ч

"-ах = . (11)

Подставляя в эту формулу численные значения входящих в нее величин (измеренные в кг и ж) для воздуха, начальное состояние которого определяется температурой 15°С и нормальным атмосферным давлением, мы получим:

/2-1,405 10ш Y 0,405 0,125 -757 ж/сек.

Зависимость скорости w от давления р графически изображена на рис. 215. На этом же рисунке изображена кривая v = (р{р), связывающая удельный объем v = давление р при адиабатическом изменении состояния. Заштрихованная площадь представляет собой интеграл

V dp =Pi-Р.

В дальнейшем мы будем рассматривать только адиабатические изменения состояния, при которых плотность и давление идеального газа связаны между собой соотношением:

Р = Р1-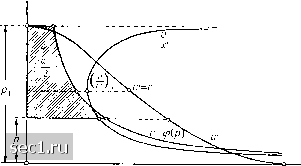

Рис. 215. Зависимость удельного объема v, скорости течения w и отношения от давления р

Условие неразрывности установившегося движения сжимаемой жидкости требует, чтобы через каждое поперечное сечение струйки газа в одну секунду протекала одна и та же масса (§3 гл. II), т.е. чтобы вдоль струйки газа соблюдалось уравнение

Fpw = const.

(12)

Отсюда мы имеем:

const constw

Следовательно, зависимость поперечного сечения F струйки газа от давления р изображается функцией (третья кривая на рис. 215). Характер связи между F ир можно выяснить, исходя из уравнений (10) и (12), следующим образом. Когда давление р равно pi скорость w = О, и поэтому поперечное сечение F = оо. При уменьшении р скорость w постепенно возрастает, однако плотность р изменяется при этом сначала незначительно, следовательно, поперечное сечение F струйки газа уменьшается. В дальнейшем, после того как давление р делается очень малым, скорость w приближается к своему максимальному значению Wmax и поэтому изменяется сравнительно слабо, но зато плотность р уменьшается очень сильно; это означает, что при неограниченном уменьшении р поперечное сечение F увеличивается и стремится к бесконечности. Очевидно, что при таком характере изменения сечения оно должно где-то проходить через минимум. Этот минимум имеет место при том давлении р*, при котором относительное прира-