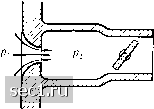Рис. 219. Истечение сжатого воздуха из отверстия через дополнительную камеру с вентилем

В том, что при истечении из простого отверстия в условиях, допускающих возникновение сверхзвуковой скорости, в нем устанавливается постоянное давление при любом противодавлении, легко убедиться при помощи рассуждений предыдущего параграфа о распространении давления. Предположим, что к выходному концу отверстия примыкает камера, давление в которой может регулироваться при помощи вентиля или другого подобного приспособления (рис. 219). Пусть давление р2 в этой камере больше критического давления р. Если открыть вентиль, то давление р2 в камере понизится и образуется волна разрежения, двигающаяся к отверстию. Эта волна изменяет состояние течения в отверстии - скорость истечения увеличивается. При дальнейшем понижении давления р2 скорость истечения будет продолжать увеличиваться, но лишь до тех пор, пока не будет достигнута звуковая скорость. Новое понижение давления не изменит состояния течения в отверстии. В самом деле, скорость распространения этого понижения давления не может превысить скорости звука, и поэтому оно не достигнет отверстия, следовательно, состояние течения в нем, начиная с момента достижения звуковой скорости, будет оставаться неизменным.

Для получения правильной сверхзвуковой струи шведский инженер Лаваль (Laval), конструируя свою паровую турбину, применил насадок особой формы, изображенный на рис. 220а и называемый теперь соплом Лаваля. Такие насадки имеют большое практическое значение, поэтому явления, происходящие в них при течении газа, очень подробно изучены и теоретически и экспериментально. Результаты этого изучения позволили получить ответ на многие принципиальные вопросы движения газов и паров.

Здесь мы рассмотрим только такое течение через сопло Лаваля, при котором можно пренебрегать трением. Пусть давление pi до сопла задано. Тогда значения скорости w и отношения , соответствующие каждому давлению р, меньшему pi, могут быть либо вычислены по формулам, либо отсчитаны по графикам на рис. 215. Так как расход газа, т.е. количество его массы, протекающей в одну секунду, равен

М = Fpw = Ff,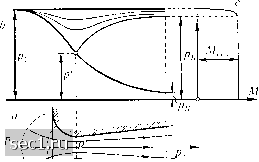

Рис. 220. Течение через сопло Лаваля

то для каждого заданного расхода М можно вычислить значения , соответствующие определенным значениям площади поперечного сечения F. Зная же , можно из рис. 215 найти соответствующие значения давления. Очевидно, что при нормальном режиме работы сопла минимум поперечного сечения струнки газа, следовательно, и минимум функции должны совпадать с минимумом поперечного сечения сопла. При таком режиме расход получается максимальным и определяется, как и при истечении из простого отверстия, формулой (14). Найденное указанным способом изменение давления вдоль оси сопла (от значения pi до самого низкого конечного давления р„) изображено на рис. 2206 жирной линией. Но так как, согласно рис. 215, каждому значению соответствуют всегда два разных давления, то в расширяющейся части сопла - после самого узкого поперечного сечения - давление может изменяться также по второй кривой, изображенной на рис. 2206 тонкой линией и ведущей к верхнему конечному давлению рв-Найдем теперь изменение давления вдоль оси сопла при меньших расходах М; мы получим кривые, вычерченные на рис. 2206 тонкими линиями и оканчивающиеся ординатами, большими рв- Изменение расхода в зависимости от противодавления р2 в конце сопла изображено на рис. 220с. При уменьшении противодавления от значении р2 = pi до значения р2 = Рв, расход возрастает от нуля до Мтах- Как только расход достигает своего максимального значения, в самом узком поперечном сечении сопла устанавливается звуковая скорость течения. Следовательно, даже не зная в точности, какие явления происходят в этом

месте, можно предполагать, что дальнейшее понижение противодавления не влияет на часть потока, расположенную вверх по течению от самого узкого места сопла, и поэтому теперь расход должен оставаться постоянным. Многочисленные опыты хорошо подтверждают это предположение.

Из предыдущих рассуждений следует, что если в газе при движении через сопло давление р уменьшается от значения pi до значения р2, лежащего между рв и р„, то обязательно должна происходить потеря энергии. А. Стодола (A.Stodola), наблюдая за изменением давления в таких потоках, обнаружил, что в них возникают прерывные изменения давления, так называемые скачки уплотнения, предсказанные теоретически Риманом (см. конец §2). При скачках уплотнения действительно возникает потеря энергии, следовательно, изучение их на основе уравнений, выведенных для потоков без потерь энергии, невозможно. Для вывода уравнений, пригодных для исследования скачков уплотнения, необходимо исходить из теоремы о количестве движения (§ 13 гл. II) в сочетании с теоремой об энергии для течений, сопряженных со значительными изменениями объема и с сопротивлениями.

В связи с большой важностью последней теоремы для изучения сжимаемых потоков, мы посвятим ей весь следующий параграф.

§ 4. Теорема об энергии для сжимаемых потоков при наличии сопротивлений. При движении газов сопротивление оказывает двоякое действие: во-первых, оно механически тормозит поток, а во-вторых, механическая энергия, затраченная на его преодоление, частично возвращается в поток в виде тепловой энергии. Таким образом, в потоках сжимаемой жидкости, в противоположность потокам несжимаемой жидкости, имеется возможность часть энергии, затраченной на преодоление сопротивления, вновь использовать при дальнейшем расширении.

Выделим в установившемся потоке газа некоторую область и вычислим изменение энергии массы газа, заключенной в этой области. Удобнее всего за такую область взять отрезок трубки тока (см. рис. 73 на стр. 114). Так как мы рассматриваем установившееся движение, то изменение состояния выделенной массы газа в течение промежутка времени dt заключается только в том, что через сечение А из трубки тока выходит элемент массы

dm, = PaFaWa dt, (15)