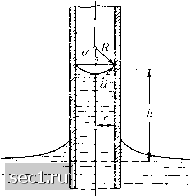Рис. 24. Подъем жидкости в капиллярной трубке

Если в жидкость опустить узкую трубочку, то в зависимости от величины краевого угла а уровень жидкости в трубочке будет либо выше, либо ниже уровня жидкости вне трубочки (рис. 24). Примем для упрощения расчета, что поверхность жидкости в трубочке имеет форму шарового сегмента; такое допущение тем точнее, чем меньше радиус трубочки г по сравнению с высотой h подъема жидкости. Тогда, согласно рис. 24, мы получим для радиуса шарового сегмента величину

cosa

Подставляя это значение R в равенство (21), мы найдем высоту подъема жидкости в трубочке:

2Ci2 cos а

(23)

72-71

Из этой формулы следует, что в трубочках с очень малым радиусом г высота подъема h может быть очень большой (всасывающее действие промокательной бумаги, мелкопористой глины и т. п.). Подставляя в равенство (23) вместо cos а его значение из формулы (22) и умножая обе части равенства на тгг, мы получим очень наглядное уравнение

(72 - 7i)rr2/i = (Ci3 - С23) • 27ГГ,

согласно которому вес столба жидкости в трубочке за вычетом потери вследствие поддерживающей силы воздуха равен результирующей сил поверхностного натяжения на стенках трубочки.

Если поверхность трубочки предварительно смочена жидкостью, то при составлении уравнения равновесия надо заменить разность Ci3 - С23 через С12, что приводит к равенству

cos а = 1.

Следовательно, в этом случае а = О, и высота подъема принимает наибольшее значение, равное

Ci2 = 2(72 -yi)hr.

Измеряя h и г, мы можем определить при помощи этой формулы величину Ci2. О другом способе определения капиллярной постоянной, основанном на измерении капиллярных волн, будет сказано в § 16 гл. П.

Для примера приведем некоторые значения капиллярной постоянной С при 20°С:

Вода относительно воздуха С = 72,5 дин/см Масло » » С = 25 -г 30 дин/см

Ртуть » » (7 = 472 дин/см.

Глава 2

Кинематика жидкостей. Динамика жидкостей, лишенных трения

§ 1. Предварительные замечания. Движения жидкостей и движения газов имеют столь много общих свойств, что целесообразно изучать те и другие совместно. Правда, газы обладают значительно большей сжимаемостью, чем жидкости. Однако при движении газа вопрос заключается не в том, в какой мере газ вообще может сжиматься, а в том, насколько он в действительности сжимается при рассматриваемом движении. Для значительного сжатия газа необходимо значительное изменение давления. Между тем при небольших и умеренных скоростях, а также при умеренном протяжении движущейся массы газа в высоту давление изменяется по сравнению со своим средним значением очень немного, и поэтому соответствующие изменения объема настолько малы, что ими в большинстве случаев можно для упрощения расчетов пренебрегать. Тогда течения газа ничем не будут отличаться от течений несжимаемой жидкости.

В самом деле, как мы увидим ниже, в § 5, при движениях атмосферного воздуха со скоростью до 50 м/сек и при условии, что протяжение воздушного потока в высоту не превышает 100 м, изменения объема при обычной температуре не превышают 1%. Только при скорости 150 м/сек они достигают круглым числом 10%. Но при скоростях, близких к скорости звука (около 340 м/сек), изменения объема достигают большой величины и потому заметно влияют на характер течения.

Наконец, при скоростях, больших скорости звука, характер течения становится совершенно иным по сравнению с обычным поведением несжимаемых жидкостей.

В настоящей и следующей главе мы будем рассматривать, главным образом, течения без заметного изменения объема. Для того чтобы при этом не говорить каждый раз, что все сказанное относится в равной мере и к жидкостям, и к газам, мы будем применять во всех случаях только слово жидкость как собирательное понятие и для жидкостей.