+ ы--рс = const. (27)

Для идеальных газов значения нив определяются соотношениями (19) и (20). Подставляя эти значения в уравнение (27), мы получим:

Н--= const (28)

+ СрТ = const (29)

(напомним, что удельную теплоемкость Ср следует измерять в единицах работы, см. §4). Из уравнения (29) следует, что при движении идеальных газов понижение температуры по сравнению с начальным состоянием зависит только от скорости течения в рассматриваемом месте, но не от величины сопротивления. Если скорость течения везде незначительна, как это наблюдается в потоках с очень большим сопротивлением, то расширение газа при его движении происходит при постоянной температуре. Работа расширения при таком движении газа

Preiswerk е., Mitteilungeii aus dem Institut fur Aerodynamik an der e.T.H. Zurich №7 (1938).

гл. II) очевидно. В самом деле, при перетекании воды через плотину скорость движения вала играет такую же роль, как скорость звука при течении газа через сопло. Прейсверк исследовал эту аналогию с математической точки зрения и показал, что движение воды над плоским дном в случае, когда горизонтальные размеры потока велики по сравнению с глубиной, в количественном отношении совпадает с плоским течением гипотетического газа, для которого отношение удельных теплоемкостей равно >г = 2. При этом глубина потока в каждом месте соответствует плотности газа и одновременно - температуре газа (так как >г = 2).

§ 6. Движение газа при наличии сопротивлений, а) Установившееся течение. В установившемся потоке газа при наличии сопротивлений, но при отсутствии теплопередачи через стенки, ограничивающие поток, полная энергия остается постоянной, так как работа трения полностью преобразуется в теплоту. В большинстве случаев разности высот не играют никакой роли, поэтому уравнение энергии (17) принимает вид:

df Grashof, Theoretische Maschinenlehre, т. I, Leipzig, 1875, стр. 592; см. также Zeuner, Techn. Thermodynamik, т. I, изд. 2, Leipzig, 1900, стр. 261.

целиком преобразуется в работу трения, и теплота, возникающая вследствие трения, возмещает охлаждение, возникающее вследствие расширения. Такое же явление наблюдается и в том случае, когда поток газа, имеющий значительную скорость, быстро теряет ее вследствие большого сопротивления.

Действительные газы немного отклоняются от такого поведения. Впервые это показали В. Томсон (W. Thomson) и Джоуль (Joule). Они заставляли протекать воздух под большой разностью давлений через ватную пробку и обнаружили, что при этом происходит небольшое охлаждение воздуха, которое они объяснили молекулярным притяжением. Для воздуха при обычной температуре это охлаждение равно 1/4° С на каждую атмосферу, однако при низких температурах оно значительно больше. На таком охлаждении газа, между прочим, основано действие машины Линде для сжижения воздуха.

Для математического исследования течения газа в трубе с сопротивлением следует к уравнению энергии (17) или (28) присоединить уравнение неразрывности и дополненное уравнение Бернулли (23) и, кроме того, ввести некоторое допущение относительно математического выражения для работы сопротивления R.

Выполнение такого исследования для течения через сопло Лаваля показывает, что поправки для скорости и давления по сравнению с прежними результатами в большинстве случаев не очень велики. В частности, звуковая скорость достигается не в самом узком поперечном сечении сопла, а немного позади него и при этом при более низком давлении. Несколько подробнее мы остановимся, не приводя вычисле-ний, на течении газа через трубу постоянного поперечного сечения.

Предварительно рассмотрим такое течение с сопротивлением, при котором скорость W остается постоянной; тогда, согласно уравнению (28),

pv = const. (30)

Так как в этом случае сопротивление преодолевается за счет падения давления в направлении течения, то из уравнения (30) следует, что удельный объем возрастает в направлении течения, следовательно, на основании уравнения неразрывности, возрастает и поперечное сечение потока. Для того чтобы от этого случая перейти к течению в трубе с постоянным поперечным сечением, следует сузить только что рассмотренный расширяющийся поток до постоянного поперечного сечения. При условии, что скорость потока меньше скорости звука, такое

сужение влечет за собой увеличение скорости и, следовательно, новое понижение давления и новое увеличение удельного объема. Это новое понижение давления тем сильнее, чем больше скорость течения приближается к скорости звука (см. кривую на рис. 215). Скорость звука с, соответствующая критическому давлению (§ 3), является в данном случае наивысшей скоростью, достижимой в конце трубы.

При движении со сверхзвуковой скоростью, которая может быть достигнута, конечно, только путем предварительного прохождения газа через поставленное перед трубой сопло Лаваля, сужение расширяющегося потока влечет за собой уменьшение скорости и повышение давления. Скорость звука с, соответствующая критическому давлению, по-прежнему является предельной достижимой скоростью при непрерывном изменении давления. Однако эта предельная скорость может быть достигнута в действительности только при условии, что труба имеет вполне определенную, не очень большую длину, зависящую от начального состояния газа и величины сопротивления трения. В трубе же с большей длиной происходит где-либо внутри трубы скачок уплотнения, скорость течения из сверхзвуковой делается дозвуковой и дальнейшее течение происходит так, как было описано выше для случая дозвуковой скорости.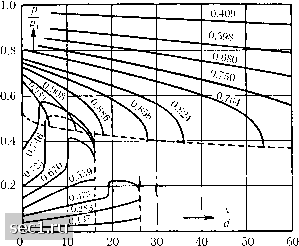

Рис. 228. Изменение давления вдоль трубы при течении газа