Рис. 278. Распыление струи горючего

Сравнение с опытами Гохшвендера (см. сноску на стр. 429) показывает, что «число» в этой оценке имеет значение, приблизительно равное 10. Для v следует подставить среднее значение скорости капель относительно воздуха (эта скорость во время процесса распыления, очевидно постепенно уменьшается). Формула (6) ясно показывает, какую роль в распылении играют скорость вспрыскивания и плотность воздуха. При равных скоростях вспрыскивания v степень распыления тем выше, чем больше плотность воздуха в цилиндре.

Вязкость увеличивает время, необходимое для раздробления больших капель на мелкие, однако учесть ее количественное влияние теоретическим путем до сих пор не удалось.

Выяснению процесса распыления горючего в дизельмоторах посвящено много опытных исследований. На рис. 278 изображена фотография распыленной струи, полученная при вспышке искры. Распыление производилось при помощи жиклера, изображенного в увеличенном виде на рис. 279.

Распыление воды применяется в дождевальных установках, устраиваемых для поливки полей и огородов. Для получения хорошего распыления перед отверстием насадка, из которого вылетает струя. Рис. 279. Жиклер для распыления устанавливается наклоненная под горючего

небольшим углом пластинка. Эта пластинка вызывает разбрасывание струи в виде веера и последующее быстрое распадение ее па капли. Еще

более эффективно действуют распыляющие насадки КерТИНГа, в кото-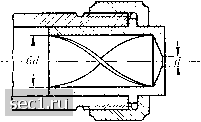

Многочисленные снимки распыления струй горючего имеются в статье О S ch at Z W., Deutsche Kraftfahrtforschung, № 57 (1941); см. также Photographie und Forschung, T. 3 (1941), стр. 170. Снимки, полученные при помощи лупы времени, имеются в статье Holfelder О., VDI-Forschungsheft 374 (1935) (здесь же даны снимки воспламенения и сгорания распыленной струи). Далее, см. BlumeK., Forschung, т. II (1941)), стр. 284, и Deutsche Kraftfahrtforschung, №53 (1941).

Поверхность маленьких пузырьков в основном ведет себя как твердая поверхность, поэтому к таким пузырькам закон Стокса приложим в своей обычной форме. Случай подвижной поверхности также исследован теоретически; для таких пузырьков, если пренебречь вязкостью содержащегося в них воздуха, получается скорость подъема, в 1,5 раза большая, чем по закону Стокса (см., например, Handbuch der Experimentalphysik, т. IV, часть 2, стр. 346).

HoferK., VDI-Forschungsheft №138 (1913), стр. 3. Подробные библиографические указания по этому вопросу имеются в статье Р i ске г t F., Forschung, т. 3 (1932), стр. 308.

рых воде, до ее подхода к узкому выходному сечению, сообщается при помощи специального приспособления мощное циркуляционное течение вокруг продольной оси насадка. По мере подхода циркулирующего потока к выходному сечению, т. е. при уменьшении радиуса этого потока, окружная скорость его значительно увеличивается (см. сказанное в §6 гл. II по поводу спиральной камеры); поэтому при выходе струи из насадка она расширяется в виде конуса и быстро распыляется. Распылитель, изображенный на рис. 279, действует именно таким способом. Существуют и другие конструкции распылителей, позволяющие осуществлять распыление под большим углом.

с) Пузыри воздуха в воде. Статическая подъемная сила пузыря воздуха в воде равна по своему численному значению весу капли воды такого же диаметра в воздухе. Поэтому для определения скорости подъема воздушных пузырей сферической формы можно применять формулы такого же вида, как выведенные в пункте а) для падения капель воды в воздухе. Необходимо только учесть, что вязкость воды при средних температурах круглым числом в 60-80 раз больше вязкости воздуха, а плотность воды приблизительно в 800 раз больше плотности воздуха.

Имея это в виду, мы получим следующие приближенные формулы, которые после подстановки значений диаметра в мм, дают скорость в м/сек:

a) для d 0,16мм V = 0,4rf и 0,5rf (закон Стокса)

b) для d 1мм V = число • л/rf (закон Ньютона).

В последней формуле при прямом восходящем движении пузырей и при с = 0,4 до 0,5 «число» должно было быть равно от 0,16 до 0,18. Однако в действительности маленькие пузыри поднимаются вверх не строго вертикально, а с отклонениями от вертикали то в одну, то в другую сторону, а иногда - по винтовой линии, причем форма их обычно все время неправильно меняется. Согласно неопубликованным еще

о О

0,01 0,1 0,7 см"

10см

Рис. 280. Формы пузырьков воздуха, поднимающихся в воде (в 1/2 натуральной величины)

Рис. 281. Пузырь воздуха в вертикальной трубе

опытам В.Мюллера (W.Miiller) для пузырьков, равновеликих по объему с шариками диаметром и от 1 до 2,5 мм, указанное выше «число» следует взять равным 0,127. Для значений rf от 3 до 8 мм форма пузырьков при движении так быстро меняется, что скорость подъема получается почти постоянной, изменяясь только в пределах от 0,21 до 0,22 м/сек. Для значений rf свыше 12 мм шарики принимают форму довольно плоского купола, практически не меняющуюся при движении; в этом случае «число» следует принять равным 0,068 (соответствующий коэффициент сопротивления равен с = 1,7). На рис. 280 изображены формы пузырьков по снимкам Мюллера. Около каждого пузырька указан его объем; шарики с таким же объемом имели бы диаметр, равный соответственно 2,7; 5,7; 11,0; 15,6; 26,7 мм.

Если в вертикальной трубе с водой поднимается один или несколько пузырей воздуха, то при полном объеме V всех пузырей вес воды в трубе на меньше того веса, который был бы при отсутствии пузырей в столбе такой же высоты = pg- удельный вес воды). Следовательно, при заданном давлении на верхнем уровне давление в трубе

рассмотренных случаях формуле для определения скоростей подъема пузырьков удобно придать вид: для пузырьков с диаметром от 1 до 2,5 мм:

V = i,28yirf;

для пузырьков с диаметром от 12 мм:

V = 0,69Vgrf

(в качестве единицы длины для всех величин следует брать см или ж).