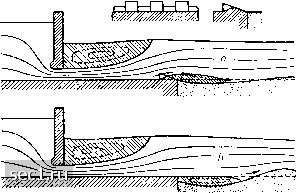Рис. 285. Образование углубления в дне реки вследствие преграждения русла щитом: а) при установке зубчатой рещетки; Ь) без такой установки. Заштрихованы те области потока, в которых происходит возвратное движение

появления таких углублении необходимо искусственным путем понизить скорость течения в придонном слое воды. Это достигается путем устройства в конце донного покрытия ряда зубцов (рис. 285а).

§ 7. Поведение тел в ускоренных потоках. Силы гидродинамического дальнодействия. В этом параграфе мы рассмотрим несколько случаев силового взаимодействия между неравномерно движущимся потоком и телом, в нем находящимся. Эти случаи представляют интерес как с практической, так и с теоретической точки зрения. Мы ограничимся рассмотрением только потенциальных течений в среде, окружающей тело со всех сторон, следовательно, не будем касаться течений с образованием поверхностей раздела.

Первый случай относится к продувке в аэродинамических трубах моделей дирижаблей. Как мы уже упомянули в § 22 гл. III, если стенки трубы параллельные, то давление в потоке вследствие его трения о стенки постепенно падает. Такое падение давления равносильно появлению добавочной силы, приложенной к модели и направленной против потока. Следовательно, эта сила увеличивает лобовое сопротивление. Так как лобовое сопротивление моделей дирижаблей очень незначительное,

K последней категории относится, в частности, течение, возникающее около крыла самолета при порывах ветра. По этому поводу см. статью К й s s п е г Н. G., ZFM, т. 22 (1931), стр. 579 и 605 [помещено также в Jahrb. d. Deutsch. Versuchsanst. f. Luftfahrt 1931, стр. 83]; далее, KussnerH. G., Luftfahrtforschung, т. 17 (1940), стр. 355.

вычитали величину V

, где V есть объем модели дирижабля; ины-

iMunkM., NACA-Rep. №114 (1921) Glauert Н., Rep. a. Mem. №1158 (1928).

Taylor G.I., Proc. Roy. Soc, т. 120 (1928), стр. 260 и Rep. a. Mem. №1160.

Конечно, вместо внесения поправок на падение давления гораздо целесообразнее устроить аэродинамическую трубу так, чтобы падения давления в направлении потока не было совсем. Для этой цели достаточно сделать трубу немного расширяющейся в направлении потока.

STollmien W., Ing.-Arch., т. 9 (1938), стр. 308.

то возникновение даже небольшого добавочного сопротивления значительно искажает результаты измерений. В первое время для исправления результатов измерения из сопротивления, измеренного на весах, др дх

ми словами, предполагали, что на модель действует кроме сопротивления еще сила, аналогичная статической подъемной силе. Однако более строгое гидродинамическое исследование, впервые выполненное Мун-ком, а затем продолженное Глауэртом и Тейлором, показало, что указанный прием дает правильные результаты только в том случае, если к объему V дирижабля прибавить еще объем V присоединенной массы (см. стр. 247). Правда, для моделей дирижаблей это уточнение почти не изменяет прежнего правила, так как присоединенная масса вытянутого эллипсоида с отношением осей 6:1 составляет только 4,5% вытесненной массы жидкости. Но для слабо вытянутого эллипсоида с отношением осей 2:1 присоединенная масса равна 20%, а для шара - 50% от вытесненной массы, поэтому в этих случаях уточнение получается очень существенным. Желающих ознакомиться со строгим доказательством и с другими примерами аналогичных течений отсылаем к работе Толлмина. В этой работе, в частности, вычислены силы и вращающие моменты, действующие на тело, обтекаемое слабо искривленным потенциальным потоком.

Перейдем к следующей задаче - выясним, как ведет себя тело, находящееся в жидкой среде, в которой имеют место переменные по времени ускорения. Пусть, например, среда, окружающая тело, получает ускорение b в направлении оси х. Вычислим, какое ускорение 6i получает при этом тело. Обозначим плотность среды через р, а плотность тела - через pi. Возмущения, вызываемые в жидкости телом, сначала не будем учитывать; в таком случае мы можем принять, что все части жидкости получают одинаковое ускорение. Этого можно достичь в действительности, например, следующим образом: заключим жидкую среду, которую будем предполагать несжимаемой, в какой-нибудь сосуд так, чтобы она заполняла его сплошь, и сообщим сосуду

Taк как такое течение возникает из состояния покоя, то оно является потенциальным течением. Приводимое ниже решение удовлетворяет граничным условиям, поэтому, согласно теореме единственности теории потенциала, оно является истинным решением.

Bjerknes V., Zeitschr. f. d. phys. u. chem. Unterricht, т. 43 (1930), стр. 1.

ускоренное поступательное движение; тогда каждая частица жидкости также будет совершать это ускоренное движение. Одинаковому ускорению b всех частиц соответствует одинаковое во всем потоке падение давления в направлении ускорения, равное

др дх

Вследствие этого падения давления тело, находящееся в жидкости, получает прежде всего «подъемную силу» в направлении ускорения, равную Vpb. Так как мы предполагаем, что плотность тела pi не равна плотности р жидкой среды, то ускорение тела bi также не будет равно ускорению жидкости Ь. Следовательно, возникнет движение тела относительно жидкости с ускорением bi - b. Этому ускоренному движению соответствует сопротивление, направленное в сторону, противоположную подъемной силе, и пропорциональное присоединенной массе pV, т. е. равное p{bi-b)V. Результирующая сила, т. е. разность между подъемной силой и сопротивлением, должна быть равна, очевидно, массе тела piV, умноженной на его ускорение bi. Таким образом, мы получаем уравнение:

p[bV -{Ъг-Ь)У] = ргУЬг, откуда находим искомое ускорение bi:

"ЬУЛУ (20)

yi + у

Это соотношение показывает, что для рг > р ускорение bi меньше ускорения 6, и наоборот. Для pi = р мы имеем, как и следовало ожидать, что bl = b. Последний результат приложим к любому объему рассматриваемой жидкости, мысленно выделенному из остальной жидкости; следовательно, этот объем вынужден под воздействием окружающей жидкости двигаться с таким же ускорением, как и остальная жидкость.

В. Бьеркнес описывает следующий простой опыт, иллюстрирующий соотношение (20). Три пробирки наполняются одинаковой жидкостью; в первую из них опускается тело с удельным весом, меньшим