скорости и других величин. Совокупность задач о движении жидкости, рассматриваемых путем одномерного представления, принято называть гидравликой. Задачи же, рассматриваемые путем трехмерного (или двухмерного) представления, составляют предмет гидродинамики. Наконец, совокупность задач о движении воздушных потоков часто называют аэродинамикой.

При трехмерном рассмотрении течений математическое выражение условия сохранения массы проще всего получить, если вычислить количества жидкости, втекающей и вытекающей в небольшой параллелепипед со сторонами dx, dy и dz (рис. 27), и приравнять эти количества друг другу. Выполним эти вычисления для несжимаемой жидкости. Обозначим проекции скорости на оси координат через и, V, W. Тогда в направлении оси х в парал-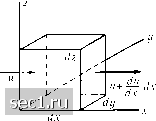

Рис. 27. К выводу уравнения неразрывности

лелепипед втекает слева в одну секунду количество жидкости dy dz • и,

а справа, где скорость и уже изменилась и стала равной и -Ь dx, вы-

текает количество жидкости dy dz{u + dx). Следовательно, в одну секунду из параллелепипеда вытекает в направлении оси х жидкости больше, чем втекает, на величину

dx dy dz

ди дх

Аналогичные выражения получаются и для направлений у и z. Условие сохранения массы требует, чтобы сумма трех полученных приращений была равна нулю, следовательно, мы получаем уравнение:

ди dv dw g дх ду dz

Это уравнение называется уравнением неразрывности.

Пусть жидкость где-либо граничит с твердым телом или с другой жидкостью. Из условия неразрывности потока следует, что нигде не должно возникать ни разрывов жидкости, ни взаимного проникновения обоих веществ. Для этого, очевидно, необходимо, чтобы составляющие скорости, перпендикулярные к поверхности соприкосновения обоих веществ, были одинаковы с обеих сторон этой поверхности. Если рассматривается неподвижное тело или твердая стенка, обтекаемая

жидкостью, то составляющая скорости жидкости, перпендикулярная к поверхности тела или к стенке, должна быть здесь равна нулю. На составляющую скорости, параллельную стенке, условие неразрывности не налагает никаких ограничений, следовательно, эта составляющая может иметь любые значения.

§ 4. Силы в движущейся жидкости. Уравнение Бернулли.

Как мы видели в гл. I, в покоящейся жидкости действуют и дают уравновешенную систему два рода сил: силы тяжести (и другие массовые силы) и разности давлений. Эти же силы действуют и в движущейся жидкости, но здесь к ним присоединяется еще трение жидкости, которое следует рассматривать как сопротивление деформации. Трение жидкости подробно будет рассмотрено в следующей главе, в этой же главе мы будем им пренебрегать. Жидкости, наиболее важные для техники (вода, воздух и др.), обладают очень малой вязкостью, и поэтому во многих случаях сопротивление, возникающее в них вследствие трения, столь мало, что пренебрежение им вполне оправдано. Кроме того, такое пренебрежение трением является и необходимым, так как только в этом случае соотношения между силами получаются достаточно простыми для того, чтобы можно было вывести из них наглядные закономерности. Поэтому обычно принято основные законы движения жидкостей выводить на основе идеализированного представления о жидкости, лишенной трения, и только после этого учитывать, какие изменения вносит наличие трения в идеальное поведение жидкости. Мы также будем следовать этому пути, причем предположим, что рассматриваемая нами идеальная жидкость обладает также свойством несжимаемости, следовательно, никаких изменений объема при Кроме того, такое пренебрежение трением является и необходимым, так как только в этом случае соотношения между силами получаются достаточно простыми для того, чтобы можно было вывести из них наглядные закономерности. Поэтому обычно принято основные законы движения жидкостей выводить на основе идеализированного представления о жидкости, лишенной трения, и только после этого учитывать, какие изменения вносит наличие трения в идеальное поведение жидкости. Мы также будем следовать этому пути, причем предположим, что рассматриваемая нами идеальная жидкость обладает также свойством несжимаемости, следовательно, никаких изменений объема при движении не происходит.

Для того чтобы найти соотношение между давлением и массовой силой, с одной стороны, и кинематическими величинами - с другой.

будем исходить из основного закона динамики: сила равна массе, умноженной на ускорение. Выделим в движущейся жидкости частицу в виде небольшого цилиндра с осью, расположенной вдоль линии тока s (рис. 28). Пусть высота цилиндра равна ds, а поперечное сечение равно dF. Тогда масса цилиндра будет pdFds.

Если в жидкости трение отсутствует, то на выделенный цилиндр действует прежде всего разность давлений. Пусть давление на основание цилиндра, расположенное выше по течению равно р, тогда сила, действующая на это основание, равна pdF. На основании цилиндра, лежащем ниже по течению, давление немного отличается от р и

равно р + ds; соответствующая сила по Рис. 28. К выводу уравне-

, ч ния Бернулли

величине равна (р -Ь ~ ds \ dF, но направлена она в сторону, противоположную силе pdF. Следовательно, вследствие разности давлений на цилиндр действует сила

pdF - (р+ ds dF = -dsdF.

Далее, на жидкость действует массовая сила (например, сила тяжести), величина которой, отнесенная к единице массы, пусть будет g. На выделенный цилиндр действует в направлении течения составляющая этой силы, равная

pdF ds g-cosa,

где а есть угол между линией действия массовой силы и линией тока.

Теперь нам остается определить составляющую ускорения в направлении течения, т. е. касательное ускорение. Пусть скорость частицы равна W. Величина w зависит от положения частицы на линии тока и от времени, следовательно, она является функцией от s и t; поэтому для касательного ускорения мы будем иметь выражение:

dw dw ds , dw

ds dt dt

или, принимая во внимание, что = w.

dw dw dw

ds dt