скорости w останется неизменной, а справа от направления w повысится. Рассмотрим теперь область жидкости, занимающую большое протяжение, и пусть в этой области при переходе от одной точки к другой величина и направление скорости w постепенно изменяются (но остаются постоянными во времени в каждой точке). Тогда, согласно только что сказанному, разность dh уровней жидкости на концах отрезка ds, перпендикулярного к скорости w, будет

dh = ds. (30)

Проследим какую-нибудь линию тока. Вследствие неразрывности должно иметь место равенство

W ds h = const,

поэтому для h = const должно быть

W ds = const.

В таком случае из равенства (30) следует, что

dh = const.

Таким образом, для любой формы свободной поверхности жидкости, определяемой системой горизонталей (т.е. линиями равного уровня), возможно такое установившееся течение, линии тока которого совпадают с горизонталями. Единственным ограничением является величина скорости w: при заданном наибольшем значении кривизны горизонталей она не должна превышать некоторого определенного значения, именно такого, при котором еще можно пренебречь трансверсальным

ускорением обусловленным кривизной траектории, по сравнению с кориолисовым ускорением. [Еще раз подчеркнем, что в основу сделанного вывода положено предположение об отсутствии трения, а также об отсутствии кривизны или наклона вращающейся поверхности. Если эта поверхность неровная, например, имеет возвышения или имеет наклон, то возникают более сложные соотношения (см. ниже).] Там, где уровень жидкости понижен (области низкого давления), направление обхода замкнутых линий тока совпадает с направлением вращения основания, наоборот, там, где уровень жидкости повышен (области высокого давления), оно противоположно направлению вращения основания. О той

роли, которую при таких течениях играет трение жидкости о поверхность основания, будет сказано в следующем параграфе.

Выше мы предполагали, что высота Н слоя жидкости над основанием везде одинакова. Если же вследствие неровности или наклона основания высота Н изменяется, но постепенно, то из теоремы Гельмгольца следует, что вертикальная составляющая вектора вращения частицы жидкости, измеренная в неподвижной системе отсчета, изменяется вдоль линии тока пропорционально Н. Предположение о постепенном изменении высоты необходимо, так как только при соблюдении этого условия (и одновременно при отсутствии трения!) горизонтальная скорость течения будет одинакова во всех точках каждой вертикали. Пусть, например, на ровной местности имеется пологое возвышение высотой h и пусть слой жидкости постоянной плотности, движущейся над местностью, имеет толщину Но. Если скорость течения жидкости во вращающейся системе отсчета постоянна по величине и направлению, то угловая скорость текущей жидкости относительно вращающегося основания равна

WoTHo = О,

следовательно, абсолютная угловая скорость будет

т. е. она равна угловой скорости вращающегося основания. Согласно сказанному выше, если только не учитывать небольших изменений высоты уровня, угловая скорость вращения над возвышением будет

Ho-h

Wa6ci - Wa6co Ft

следовательно, угловая скорость относительного вращения равна

/ / h

Это означает, в соответствии с изложенным выше, что над возвышенном возникает, во-первых, повышение давления и, во-вторых, циркуляционное течение, направленное по часовой стрелке в северном полушарии и против часовой стрелки - в южном полушарии. В атмосфере, где вместо свободной поверхности имеется постепенное понижение плотности, происходит сходное явление, отличающееся от описанного только в количественном отношении (см. § 14, п.с). Такого рода повышение давления наблюдается в действительности над местностями, расположенными высоко над уровнем моря.

Ветер, дующий поперек длинной горной цепи (рис. 288), отклоняется в северном полушарии вправо. Пусть горная цепь простирается в направлении оси у (перпендикулярной к плоскости рис. 288) и пусть до горной цепи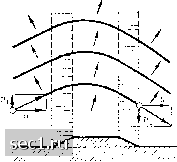

{х = xi) горизонтальные составляющие скорости ветра равны соответственно

и = и = const, ди

В таком случае

V = Vl = const. = О, и поэтому из со-

отнощения

IOTH - 2

1fdv ди\ \дх ду}

мы имеем:

Рис. 288. Обтекание гребня горы

Интегрируя от а; = Ж1 цр х = Х2, мы получим:

ду дх

V2=Vl-

dx = Vi- F,

где F есть площадь поперечного сечения через горную цепь, ограниченная слева и справа абсциссами xi и Ж2. Отсюда следует, что тангенс угла отклонения потока равен

V2-V1 2u>F и HoU

т. е. отклонение тем больще, чем меньше составляющая скорости течения перпендикулярная к горной цепи. Поэтому в морях, где течения значительно медленнее, чем ветры на поверхности Земли, отклоняющее действие длинных возвышенностей значительно сильнее, чем в атмосфере.

Отклоняющее действие длинной возвышенности (горной цепи) можно вычислить также иным путем, а именно, исходя из распределения давления. Над плоской местностью, согласно предыдущему, мы имеем:

Над гребнем возвышенности вследствие неразрывности потока скорость равна

Яо-/*

Величина тг- должна иметь здесь такое же значение, как и до возвышеннос-ду