Полагая

мы получим:

Из четырех комплексных корней этого уравнения два имеют положительные вещественные части. Этим двум корням соответствует затухание составляющих скорости и и г> по направлению вниз, следовательно, эти корни дают решение задачи для возмущений, исходящих от верхней ограничивающей поверхности.

Примером таких возмущений являются морские течения, вызванные ветрами. Два другие комплексные корня уравнения (31) имеют отрицательные вещественные части. Этим корням соответствует затухание составляющих и и v по направлению кверху, следовательно, эти корни дают решение рассматриваемой задачи, которое можно представить в следующей вещественной форме:

и = Uil-e-fcosf3z), v = U = e-fsm(3z,

a г/ = есть кинематическая вязкость. Проекция годографа результирующей скорости на горизонтальную плоскость изображена на рис. 289.

EkmanW., Dynamische Gesetze der Meeresstromungen, Innsbrucker Vortrage 1992, стр. 97.

а в направлении оси у - сила вязкости P-f (см §1, гл. III). Так как

каждый слой, согласно предположению, движется равномерно, то ускорения, за исключением кориолисова ускорения, отсутствуют. Далее мы имеем:

1 = О, = -2p.U.

ox оу

Следовательно, уравнения движения принимают вид:

и-

и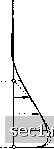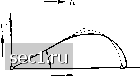

Рис. 289. Ламинарное приземное тече- Рис. 290. Турбулентное приземное те-ние чение

Полученная кривая называется спиралью Экмана. Мы видим, что направление ветра у поверхности земли отклонено от направления высотного ветра на 45°.

Для решения аналогичной задачи в случае турбулентного движения следует ввести в расчет вместо вязкости \i коэффициент турбулентного перемешивания А [§ 4, п. е) гл. III]. Так как этот коэффициент во много раз больше, чем \i и приблизительно пропорционален скорости ветра, то пограничный слой получается значительно толще, чем при ламинарном движении, причем тем более толстым, чем больше скорость ветра. Кроме того, поскольку величина коэффициента А не постоянна по высоте z, для распределения скорости в пространство получаются иные формулы, чем при ламинарном движении. В частности, наибольший градиент скорости получается, как вообще всегда при турбулентных течениях, вблизи поверхности земли. Поэтому средняя скорость в пограничном слое больше, чем при ламинарном движении, что несколько сглаживает разность между кориолисовыми силами вблизи поверхности земли и на высоте; этим и объясняется, что при турбулентном движении отклонение направления ветра в зоне трения от направления высотного ветра меньше, чем при ламинарном движении. Проекция годографа скоростей на горизонтальную плоскость изображена на рис. 290.

Подчеркнем, что полученные результаты являются точными толь-

Тх = 2uj j pv dz, (32)

Ту = 2uj j p(U - u) dz. (33)

в этих формулах h означает ту высоту, на которой величины U - и и V можно считать равными нулю. Результирующее касательное напряжение должно иметь направление ветра в зоне трения, следовательно, угол а между этим направлением и направлением высотного ветра определяется из соотношения:

Согласно сказанному в § 5, п. d) гл. III, касательное напряжение при турбулентном течении вдоль шероховатой поверхности приблизительно пропорционально квадрату скорости. Из этого в сочетании с уравнением (32) следует, что высота пограничного слоя при увеличении скорости ветра возрастает приблизительно пропорционально этой скорости.

Дальнейшие точные вычисления невозможны, так как пока мы еще не знаем точных закономерностей, имеющих место при ускоренных турбулентных течениях. Поэтому мы ограничимся здесь только приближенной оценкой.

Примем, что вблизи поверхности земли составляющая скорости и равна

u = u[f-y\ (35)

ко для случая прямолинейных установившихся изобар. В действительности же изобары обычно непрямолинейные и изменяются во времени, поэтому измерения скорости и направления ветра, производимые путем наблюдения за движением шаров-пилотов или путем записи курса и скорости свободных аэростатов, дают результаты, более или менее отклоняющиеся от указанных выше теоретических значений.

Ь) Для получения численных соотношений необходимо знать составляющие Тх и Ту касательного напряжения на поверхности земли. Общие формулы для этих составляющих легко вывести, исходя из значений кориолисовых сил в приземном течении. Мы получим: