с. ТЕЧЕНИЯ В РАССЛОЕННЫХ ВЕСОМЫХ ЖИДКОСТЯХ 493 интеграл записывается следующим образом:

- J gradp-ds,

где ds есть элемент жидкой линии. Согласно теореме Стокса, этот интеграл, взятый вдоль замкнутой линии, равен поверхностному интегралу

rot gradpj dF,

взятому по площади F, ограниченной замкнутой линией. Но мы имеем: rot(igradp) = V X (igradp) =

; n 1

= (V-j X gradp-l- -V X gradp.

Так как ротация градиента равна нулю, то последний член в равенстве (59) отпадает, и мы получаем:

- У i gradp • ds = - j j grad x gradp • dF.

Обозначая циркуляцию через Г, мы будем иметь:

= - j j grad i X gradp • dF. (60)

Если grad i везде параллелен gradp, то подынтегральное выражение равно нулю, и мы по-прежнему получаем, что

Если же поверхности р = const vi v = const, каждая из которых перпендикулярна к соответствующему градиенту, пересекаются друг с другом, то правая часть формулы (60) не равна нулю.

В. Бьеркнес дал для интеграла в правой части формулы (60) очень наглядное геометрическое толкование. Пусть проведены все поверхности р = const с интервалом Др и все поверхности ц = i = const {v есть

объем единицы массы) с интервалом Дг;; тогда каждая пара соседних поверхностей р = const образует с каждой парой соседних поверхностей V = const трубку, поперечное сечение которой представляет собой параллелограмм (рис. 297). В.Бьеркнес показал, что интеграл в правой части формулы (60) пропорционален числу трубок, окруженных жидкой линией.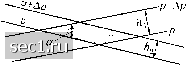

Для доказательства вычислим прежде всего площадь поперечного сечения трубки. Это поперечное сечение представляет собой параллелограмм, плоскость которого перпендикулярна к линиям пересечения обоих семейств р = const и v = const. Если hi есть расстояние между двумя соседними поверхностями р = const, а /i2 - между двумя соседними поверхностями v = const, то площадь параллелограмма, очевидно, равна

Рис. 297. Трубка, образованная пересечением поверхностей р = const и V = const

hih2 sina

Если вместо поперечного сечения, перпендикулярного к стенкам трубки, взять косое сечение, то мы получим другой параллелограмм, наклоненный относительно первого на некоторый угол /3. Площадь наклонного параллелограмма, очевидно, равна

cos/3

Так как

то мы имеем

Др =/ll • I gradpl, Дг; =/i2 • I gradl.

ApAv

gradpjl gradiij sin a cos/3

Знаменатель этого выражения совпадает с подынтегральным выражением в формуле (60). В самом деле, синус появляется в результате векторного произведения, а косинус - в результате скалярного произведения. Число параллелограммов с площадью / на единице площади равно

„=1.

Полное число таких параллелограммов на площади F, замыкаемой жидкой линией, будет

I gradpj I grad г; sin а cos /3 dF ApAv

с. ТЕЧЕНИЯ В РАССЛОЕННЫХ ВЕСОМЫХ ЖИДКОСТЯХ 495 Сравнивая это равенство с формулой (60), мы получим:

= ep-AvN. (61)

Знак в каждом отдельном случае легко определить из того соображения, что более плотные части жидкости стремятся двигаться вниз, а менее плотные - вверх. Теорема Бьеркнеса пригодна главным образом для качественного исследования. Применение ее для количественного исследования затрудняется тем, что обычно поле давлений ускоренного течения точно не известно. Исключение составляют течения в таком пространстве, горизонтальное протяжение которого во много раз превышает вертикальное протяжение. Этот случай имеет место в большинстве метеорологических приложений. При течениях в таком пространстве вертикальные ускорения вследствие условия неразрывности малы по сравнению с горизонтальными ускорениями, и поэтому давление на каждой вертикали можно определять на основании законов гидростатики. Для вычислений, однако, целесообразно пользоваться не тем интегралом, который получился в правой части формулы (60), а его исходной формой, т.е. интегралом

- J gradp-ds.

Так как теперь

I gradpl = pg,

то при интегрировании вдоль вертикальных отрезков жидкой линии получается просто p{hi - /12); при интегрировании же вдоль отрезков жидкой линии, расположенных на изобарных поверхностях, получается нуль.

Ь) Внутренние волны в несжимаемой среде. В каждой расслоенной среде, находящейся в устойчивом состоянии, возможны внутренние волновые движения. До настоящего времени исследованы главным образом простые формы таких движений, в том числе так называемые ячейковые волны. При таком волновом движении все пространство разбивается на отдельные ячейки, как бы ограниченные жесткими стенками. Колебания во всех ячейках происходят с одинаковой частотой. Наиболее простым случаем являются плоские стоячие волны в несжимаемой расслоенной жидкости.