И случае же волн на свободной поверхности воды период колебаний, как это следует из равенств (60) и (62) на стр. 129 и 129, равен

g

т.е. зависит от длины волны A.

В общем случае ячейковые волны имеют три измерения. Путем наложения друг на друга ячейковых волн с разными длинами Л;, Aj, и получаются волны более общего вида, причем не всегда ячейковые. Эти волны до настоящего времени мало изучены. Практически интересный случай таких волн будет рассмотрен ниже, на стр. 501.

Таким образом, мы видим, что в расслоенной весомой жидкости с плотностью, убывающей снизу вверх, возможны очень разнообразные колебательные движения, следовательно, поведение такой жидкости совершенно не похоже на поведение однородных жидкостей. Решения, получаемые при исследовании колебаний в расслоенной жидкости, в отличие от аналогичных задач для однородных жидкостей, не однозначны. Они делаются однозначными только тогда, когда принимаются во внимание силы трения или когда возникновение движения из состояния полного покоя расчленяется на ряд последовательных этапов. Математическое исследование обоих этих случаев наталкивается на большие затруднения.

с) Внутренние волны в сжимаемой среде. Исследование ячейковых волн, возникающих в сжимаемой расслоенной среде, например, в расслоенном весомом газе, температура которого везде одинакова, труднее, чем изучение таких же волн в несжимаемой среде, так как при вычислениях необходимо учитывать, что каждая отдельная частица газа при колебательном движении адиабатически изменяет свое состояние. Из уравнения (3) гл. IV следует, что в этом случае изменения давления Др связаны с изменениями плотности Ар соотношением

Др = с1,Ар,

где Сзв есть скорость звука, равная

сравнению с SttH, получается практически одинаковый, не зависящий от Лз;, период колебаний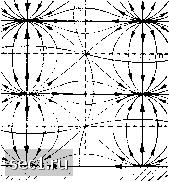

Рис. 300. Стоячие ячейковые волны звукового типа

Как показывают исследования, в сжимаемой среде возможны два типа ячейковых волн. Волны первого типа характерны тем, что они колеблются сравнительно медленно и что основной причиной их возникновения являются перемещения центра тяжести частиц жидкости. Ячейковые волны, возникающие в несжимаемой среде, принадлежат к этому же типу. Волны второго типа колеблются значительно быстрее, и основной причиной их возникновения является последовательное сжатие и расширение частиц жидкости. Линии тока волн второго типа изображены на рис. 300. Если + /3

велико по сравнению с -следовательно, если A,, или Х, или оба они Н

малы по сравнению с 2тгН, где теперь Н означает высоту однородной атмосферы, равную круглым числом 8000 м (см. стр. 28), то для круговой частоты обоих типов волн получаются следующие приближенные формулы:

(67) (68)

В этих формулах а и /3 имеют тот же смысл, что и раньше, а яг есть отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме. Мы видим, что формула (67)

отличается от формулы (64) только множителем ~ , если не считать некоторой разницы в последнем слагаемом знаменателя, которое нами в формулах (67) и (68) не выписано.

От стоячих волн можно перейти к бегущим волнам совершенно так же, как это было сделало в пункте Ь). Скорость бегущих волн второго типа равна

Bjerknes V., Physikalische Hydrodynamik, Berlin 1993, стр. 341.

A = 27rt f. (70)

Полученное решение - неоднозначное, но оно делается таким, если ввести дополнительно требование об апериодическом характере результирующего движения на наветренной стороне горы. Заметим, что такое же требование вводится в родственных задачах гидродинамики*. Формула (70) приближенно применима также к случаю политропической атмосферы {р ~ р"-), необходимо только подставить в нее вместо величину а Н принять равным высоте соответствующей

iMargules М., Sitz.-Ber. d. Wiener Akad. Па, т. 99 (1890), стр. 204, т. 101 (1892), стр. 597, т. 102 (1893), стр. 11 и 1369; см. также К os chmi е de г Н., Dynamische Meteorologie, изд. 2, Leipzig 1941, стр. 297; в этой книге имеются подробные библиографические указания [первое издание переведено на русский язык: КошмидерГ., Динамическая метеорология, Москва 1938 {Прим. перев.)]

Lyra G., Beitr. z. Physik. d. freien Atmosphare, т. 26 (1940), стр. 197; см. также К о s chmi е der Н., Dynamische Meteorologie, изд. 2, стр. 318.

LyraG., ZAMM, т. 23 (1943), стр. 1. Из этой работы взят приводимый ниже рис. 301; в ней имеются также многочисленные другие рисунки.

"См. в связи с этим рис. 2726 на стр. 427.

т.е. больше скорости звука. Эти волны можно рассматривать, как результат наложения друг на друга двух звуковых волн, фронты которых наклонены относительно вертикали на углы

Если ввести угол 7 в формулу (69), то мы получим:

COS 7"

Колебания в земной атмосфере в предположении, что она изотермическая, впервые подробно были изучены Маргулесом.

С практической точки зрения представляет интерес возмущение, вызываемое в горизонтальном потоке воздуха, движущемся со скоростью [/, препятствием в виде горной гряды умеренной высоты, расположенной перпендикулярно к направлению потока. Лира исследовал такой случай для изотермической атмосферы и показал, что возмуще-

ние выражается суммой бесселевых функций от аргумента --, ум-

ноженных на круговые функции от Lp, и на е/я г = \/х + есть расстояние от центра возмущения на поверхности земли, ip - угол (tg( = ) и Л - длина волны, которая приближенно равна